Veremos cómo encontrar puntos racionales del círculo geométricamente y cómo hacerlo puramente algebraico.
El teorema se puede explicar con un poco de teoría algebraica de números y teoría de Galois, lo que trataré de resumir en el contexto de este teorema sólo para poder entenderlo de manera informal.
Nota importante:
Si no entienden el siguiente teorema, no importa, no se asusten ni dejen de leer los interesados, todo este post será dedicado a explorar cada concepto, hablaremos un poco de teoría de Galois, de Normas, Trazas y extensiones de campos, y veremos que este teorema inofensivo nos ayudará con muchos problemas geométricos.
Teorema 90 (David Hilbert)
Sea $latex L/K$ una extensión de campos cuyo grupo de Galois $latex G:=Gal(L/K)=Aut_{K}(L) =\langle \sigma \rangle$ es cíclico y si $latex x\in L$ tiene norma $latex 1$, es decir $latex N_{L/K}(x)=1$ , entonces existe $latex y\in L$ con $latex x = \frac{\sigma(y)}{y}$
Seguramente hay muchas dudas, ¿por qué es tan importante?, vamos a analizar un problema, que es el de encontrar puntos con coordenadas racionales en una circunferencia, es decir con coordenadas $latex (\frac{a}{b},\frac{c}{d})$ con $latex a,b,c,d\in \mathbb{Z}$
Ejemplo para motivación
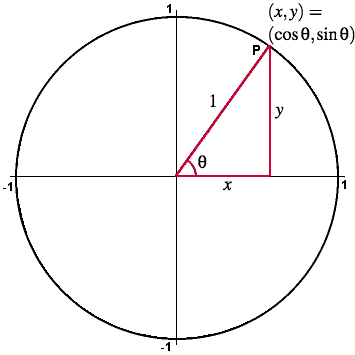
Todos sabemos que la parametrización de una circunferencia de radio 1 está dada por los puntos $latex (cos(\theta),sen(\theta) )$ con un parámetro $latex \theta$, ya que tenemos el teorema de Pitágoras que nos dice en este contexto que $latex cos^2(\theta) + sen^2(\theta)=1$ es decir, el coseno es el lado en $latex x$ y el seno el lado en $latex y$ de todos los posibles triángulos rectos cuyo ángulo en el origen es $latex \theta$ con hipotenusa $latex 1$ forma una familia infinita de triángulos que está parametrizada por una sóla variable $latex \theta$, por lo que decimos que la circunferencia es un objeto geométrico de dimensión 1.
Las coordenadas $latex (cos(\theta),sen(\theta))$ justamente por la hipotenusa estar fijada a 1, formarían todos los puntos de una circunferencia de radio 1.
Es decir, el círculo está definido justamente por triángulos de hipotenusa 1 (en rojo), con su lado en la base $latex x=cos(\theta)$ y en su altura $latex y=sen(\theta)$ por lo que es el conjunto de puntos en el plano tal que $latex x^2 + y^2 = 1$.
$latex N_{\mathbb{Q}(i)/\mathbb{Q})}(\alpha)=det(\mu^{*}_\alpha)=a^2+b^2$
Las coordenadas $latex (cos(\theta),sen(\theta))$ justamente por la hipotenusa estar fijada a 1, formarían todos los puntos de una circunferencia de radio 1.
Es decir, el círculo está definido justamente por triángulos de hipotenusa 1 (en rojo), con su lado en la base $latex x=cos(\theta)$ y en su altura $latex y=sen(\theta)$ por lo que es el conjunto de puntos en el plano tal que $latex x^2 + y^2 = 1$.
Ahora, pero como algebrista, a mi me interesan los puntos racionales de esa circunferencia, es decir, todos los puntos cuyas coordenadas son puntos racionales, es decir cuando los puntos del círculo
$latex (x,y) \in\mathbb{Q}\times\mathbb{Q}$, queremos excluir puntos como $latex (\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})$ o $latex (\frac{\sqrt{3}}{2},\frac{1}{2})$ que respectivamente corresponden cuando el ángulo del eje $latex x$ y la hipotenusa es $latex 45^{o}=\frac{\pi}{4}$ y $latex 30^{o}=\frac{\pi}{6}$ que claramente pertenecen al círculo pero tienen componentes irracionales.
Si queremos localizar puntos racionales, primero nos aseguramos de conocer un punto racional (por ejemplo el $latex (-1,0)$ , después construimos la recta que pasa por $latex (-1,0)$ y un punto en general $latex (x,y)$, es decir, vamos a variar la pendiente $latex t$ de la recta que pasa por $latex (-1,0)$ , al final, al tener este haz de rectas parametrizadas por su pendiente $latex t$ para todo $latex t \in \mathbb{Q}$ vamos a intersectar esta recta con el círculo y ver qué nos da, es decir, vamos a buscar todas las intersecciones de las rectas fijadas en un punto racional del círculo y con pendiente racional, a ver si de pura coincidencia nos da un punto racional del círculo.
La idea visual es ésta:
La recta que pasa por $latex (-1,0)$ y con pendiente parametrizada por $latex t$ está dada entonces por $latex y = t(x+1)$ , es fácil ver que esta familia de rectas para todo $latex t\in\mathbb{Q}$ son las rectas verdes en el dibujo de arriba que pasan con $latex (-1,0)$
Por otro lado, tenemos que como explicamos anteriormente, la ecuación del círculo algebraica está dada por todos los puntos $latex (x,y)$ cuya suma de sus cuadrados nos da una hipotenusa de tamaño 1, es decir $latex x^2 + y^2 = 1$.
Con esto, vamos a introducir la familia de rectas paramétrizadas por la pendiente dentro del círculo, sí, esto es que si las rectas son $latex y=t(x+1)$ entonces $latex y^2 = (t(x+1))^2$ , y si intersectamos este conjunto de soluciones en el plano con el conjunto de soluciones en el círculos nos queda $latex x^2 + t^2(x+1)^2 = 1$ que es una ecuación cuadrática, y de hecho representa explícitamente al polinomio $latex (t^2 + 1)x^2 + 2t^2x+t^2-1$.
Tenemos que este polinomio tiene como raíces a la $latex x=-1$ que ya conociamos, y también a $latex x=\frac{1-t^2}{1+t^2}$ lo cual suena ya interesante.
En otras palabras, el haz de rectas choca con el círculo en $latex x=-1$ y en $latex x= \frac{1-t^2}{1+t^2}$.
Vamos a despejar la $latex y$ en la familia de rectas dada esta nueva $latex x=\frac{1-t^2}{1+t^2}$ que obtuvimos al intersectar con el círculo y obtenemos $latex y=\frac{2t}{1+t^2}$, con esto tenemos que estas dos ecuaciones como son parte del círculo y una recta racional, pues nos dieron por suerte una función racional, por lo que la ecuación del círculo funciona con estas soluciones, $latex \Big (\frac{1-t^2}{1+t^2}\big)^2 + \Big(\frac{2t}{1+t^2}\big)^2=1$ que es fácil verificar, y tenemos una nueva parametrización con números racionales del círculo, dada por todos los puntos $latex \Big(\frac{1-t^2}{1+t^2},\frac{2t}{1+t^2}\Big)\in \mathbb{Q}\times\mathbb{Q}$ con $latex t\in\mathbb{Q}$.
¿Qué tiene que ver este ejemplo con el Teorema 90?
Vamos a contextualizar el ejemplo con las hipótesis, y ver ¿cuándo podemos parametrizar con funciones racionales? , ya que no siempre se puede hacer esto, el Teorema 90 de Hilbert nos puede decir en qué casos conviene buscar esta parametrización, y en qué caso, simplemente... no existe de manera natural (a veces existe con otras funciones modulares, o en otros espacios).
Para ello necesitamos un poco de teoría.
Embarrada de Teoría de Galois en este contexto y grupo Gal(L/K)
Vamos a describir unos ejemplos, y definiciones, sin rigor, sólo queremos por ahora entender lo que nos dice el teorema 90 de Hilbert.
Tenemos que el campo en el que trabajamos es el de los racionales $latex \mathbb{Q}$ , vamos a extenderlo a que incluya el nuevo entero algebraico $latex i$ donde $latex i^2 = -1$, por lo que tenemos.
$latex \mathbb{Q}(i) = \lbrace a+ib : x,y\in\mathbb{Q} \rbrace$
Este como pueden observar es un espacio vectorial sobre $latex \mathbb{Q}$ , son los números complejos racionales.
Vamos a ver qué es una extensión de campos pero antes una nota de cómo construir este espacio algebraicamente, ya que de esto se trata esto... de álgebra, después entraremos a la parte de extensiones de campos y teoría de Galois.
Nota de construcción algebraica de $latex \mathbb{Q}(i)$ para interesados, si no te interesa puedes omitir este párrafo:
Decimos que $latex i \in \mathbb{Q}(i)$ es un entero algebraico sobre $latex \mathbb{Q}$ ya que podemos construir este nuevo campo tomando el anillo de polinomios con coeficientes en $latex \mathbb{Q}$ módulo el ideal máximo generado por el polinomio irreducible con coeficientes en $latex \mathbb{Q}$ que tiene como raíz a $latex i$ , y esto es: $latex \mathbb{Q}(i) = \mathbb{Q}[X]/\langle X^2 + 1 \rangle = \lbrace a+bX : X^2 + 1 = 0\rbrace$.
La última construcción simplemente por el hecho de que $latex \mathbb{Q}[X]$ es un anillo (dominio euclídeo) , podemos usar el algoritmo de la división (como en la prepa la división sintética) y sólo dice que $latex \mathbb{Q}[X]/\langle X^2 + 1 \rangle$ son todos los polinomios en una variable módulo $latex X^2 + 1$ , lo que significa que todos los de la forma $latex g(X)(X^2 + 1)\equiv 0 \bmod X^2 + 1$, y como es un dominio entero si $latex g(X)\neq 0$ entonces eso implica que $latex X^2 = -1$ por lo que la variable $latex X$ en esta construcción actúa como la $latex i$ imaginaria, y así se construyen los números complejos algebraicamente.
Tenemos que la extensión de campos $latex \mathbb{Q}(i)/\mathbb{Q}$ como su construcción depende de un polinomio de grado 2 como lo hicimos anteriormente (no se puede con grado 1 ya que el campo resultante sería $latex \mathbb{Q}$ ) es un espacio vectorial de dimensión 2 con base $latex \lbrace 1,i \rbrace$.
Esta extensión $latex \mathbb{Q}(i)/\mathbb{Q}$ es normal lo que quiere decir que todos los polinomios irreducibles con coeficientes en el campo chico, es decir $latex \mathbb{Q}[X]$ que tienen alguna raiz en $latex \mathbb{Q}(i)$ entonces tienen todas ahí, en este caso es fácil, ya que si un polinomio cuadrático lo puedes factorizar, entonces lo puedes factorizar con factores lineales.
Un antiejemplo de extensión normal sería $latex \mathbb{Q}(\sqrt[3]{2})\cong \mathbb{Q}[X]/\langle X^3 -2 \rangle$ sobre $latex \mathbb{Q}$, ya que $latex X^3 - 2$ tiene como raíz $latex \alpha=\sqrt[3]{2}\ $ y también tiene $latex \alpha\omega$ donde $latex \omega = e^{\frac{2\pi i}{3}}$ y pues $latex \omega \notin \mathbb{Q}(\sqrt[3]{2})$.
Regresando a $latex \mathbb{Q}(i)/\mathbb{Q}$ donde aparte de ser una extensión normal tenemos que también es una extensión separable, lo que significa que para todo $latex \beta \in \mathbb{Q}(i)$ tenemos que el polinomio de grado mínimo de $latex \beta$ sobre $latex \mathbb{Q}$, $latex f(X)$ (es decir tal que $latex f(\beta)=0$) , tiene raíces diferentes.
Un antiejemplo de un polinomio separable sería el polinomio $latex X^3 - 2 \in \mathbb{F}_3[X]$ (con coeficientes en el campo finito de 3 elementos), ya que $latex X^3 - 2=(X+1)^3$ en ese campo, por lo que tiene una raíz triple.
Es fácil demostrar formalmente ya con estas observaciones que $latex \mathbb{Q}(i)/\mathbb{Q}$ es una extensión de campos separable y normal , por lo que decimos que la extensión es Galois.
Estas extensiones $latex L/K$ se les puede asociar un grupo , que es el Grupo de Galois, este grupo está formado por todos los Automorfismos de $latex L$, (isomorfismos de $latex \psi:L\rightarrow L$) tal que dejan a $latex K$ fijo, es decir, que $latex \psi(K)=K$, cuya operación naturalmente es la composición de funciones, el hecho de considerar que fijen a $latex K$ sirve para tomar los automorfismos interesantes, es decir, que nos permitan estudiar a $latex L$ con respecto a $latex K$.
Este grupo mide la simetría de la extensión de campos, y de hecho el numero de elementos en el grupo de Galois, está acotado por $latex [L:K]!$ es decir, por el factorial del grado de la extensión (el caso de extensión de grado infinito existe, como por ejemplo $latex \bar{\mathbb{Q}}/\mathbb{Q}$, y obviamente es un resultado diferente pero no lo necesitamos aquí)
En el caso de $latex \mathbb{Q}(i)/\mathbb{Q}$ tenemos que el grado de la extensión es 2, y lo denotamos por $latex [\mathbb{Q}(i):\mathbb{Q}]=2$ (hay teoremas que te dicen cómo acotar también por el grado del polinomio mínimo, en este caso el polinomio mínimo de $latex i$ tiene grado 2) por lo que $latex |Gal(\mathbb{Q}(i)/\mathbb{Q})|=2$.
De hecho, tenemos que $latex id\in Gal(\mathbb{Q}(i)/\mathbb{Q})$ por lo que ya tenemos un elemento de este grupo de Galois, ya que la identidad es un automorfismo.
El otro elemento es un $latex \psi:\mathbb{Q}(i)\rightarrow \mathbb{Q}(i)$ tal que si $latex z=a+bi\in \mathbb{Q}(i)$ entonces $latex \psi(z)=\psi(a)+\psi(bi)=a+b\psi(i)$ ya que $latex a,b\in\mathbb{Q}$ y $latex \psi$ es un automorfismo, y como mencionamos anteriormente $latex \psi(\mathbb{Q})=\mathbb{Q}$.
Por otro lado tenemos que $latex i^2 = -1$ por lo que $latex \psi(-1)=\psi(i^2)=\psi(i)\psi(i)=\psi^{2}(i)=-1$, esto implica que $latex \psi(i)=\pm i$ , ya que $latex (-i)(-i)=-1$ y $latex (i)(i)=-1$ .
Para la opción de $latex \psi$ tal que $latex \psi(i)=id(i)=i$ tenemos ya a la identidad, pero la otra opción $latex \psi(i)=-i$ tenemos ya el otro automorfismo, que es la conjugación por lo que.
$latex Gal(\mathbb{Q}(i)/\mathbb{Q})=\lbrace id,\psi \rbrace$.
Y como es un grupo de grado primo (2) , es cíclico, es decir está generado por 1 sólo elemento, en este caso la conjugación, ya que $latex \psi \circ \psi = id$
Normas y trazas
Para terminar de entender el Teorema 90 nos hace falta lo que es la norma.
Esto ya lo expliqué en otro post en mi blog aquí, pero doy un resumen en este contexto.
Lo que queremos es definir una manera de poder medir a los elementos de un campo $latex L$ con respecto a un valor en $latex K$ para una extensión de campos $latex L/K$
Considera la extensión $latex L/K$ y define los siguientes $latex K$-endomorfismos de $latex L\rightarrow L$ para todo elemento $latex \alpha \in L$
$latex \mu_\alpha : L\rightarrow L$
$latex z \mapsto \alpha z$
Es decir, es sólo multiplicar cualquier elemento $latex z\in L$ por $latex \alpha \in L$ , lo cual claramente es $latex K-$lineal, es decir $latex \mu_\alpha(z_1+z_2)=\mu_\alpha(z_1)+\mu_\alpha(z_2)$, por lo que le podemos asociar una matriz a $latex \mu_\alpha$, y tenemos entonces que la norma de $latex x\in L$ es:
$latex N_{L/K}(x) = det(\mu_x) \in K$
$latex Tr_{L/K}(x) = Tr(\mu_x) \in K$
Es claro que $latex N_{L/K}(xy)=N_{L/K}(x)N_{L/K}(y)$ y $latex Tr_{L/K}(x+y)=Tr_{L/K}(x)+Tr_{L/K}(y)$ por propiedades de determinantes.
Ejemplo. en $latex \mathbb{Q}(\sqrt{2})/\mathbb{Q}$
Sea $latex \mathbb{Q}(\sqrt{2})/\mathbb{Q}$ , y como espacios vectoriales fijemos la base $latex \lbrace 1, \sqrt{2} \rbrace$, entonces tenemos que si $latex \alpha=a+b\sqrt{2}\in \mathbb{Q}(\sqrt{2})$ entonces tenemos que las columnas de la matrix definida por la multiplicación por $latex \alpha$ , es decir la matriz asociada a $latex \mu_\alpha$ la podemos armar evaluando en los elementos de la base:
$latex \mu_\alpha(1) = a+b\sqrt{2}$
$latex \mu_\alpha(\sqrt{2}) = 2b+ a\sqrt{2}$
Por lo que:
$latex \mu_\alpha = \mu^{*}_\alpha = \begin{pmatrix} a &2b \\ b & a \end{pmatrix}$
Es fácil ver que si para $latex \alpha=a+b\sqrt{2}\in \mathbb{Q}(\sqrt{2})$ multiplicamos la matriz $latex \mu^{*}_\alpha$ por cualquier elemento $latex x+y\sqrt{2}\in \mathbb{Q}(\sqrt{2})$ nos da el mapeo de multiplicación por $latex \alpha$, $latex \mu_\alpha$
Es decir:
$latex \mu^{*}_\alpha \begin{pmatrix}x \\ y\end{pmatrix} = \begin{pmatrix} a &2b \\ b & a \end{pmatrix}\begin{pmatrix}x \\ y\end{pmatrix}=(ax+2by,bx+ay)$
El cual un cálculo rápido verifica que es lo mismo que esta matriz es lo mismo que el mapeo:
$latex \mu_\alpha(x+y\sqrt{2}) = \alpha(x+y\sqrt{2})=(a+b\sqrt{2})(x+y\sqrt{2}) =ax + 2by + (bx+ay)\sqrt{2}$
Por lo que tenemos que la norma y traza de $latex \alpha=a+b\sqrt{2}\in \mathbb{Q}(\sqrt{2})$ es:
$latex N_{\mathbb{Q}(\sqrt{2})/\mathbb{Q})}(\alpha)=det(\mu^{*}_\alpha)=a^2-2b^2$
$latex Tr_{\mathbb{Q}(\sqrt{2})/\mathbb{Q})}(\alpha)=Tr(\mu^{*}_\alpha)=2a$
Ejemplo. en $latex \mathbb{Q}(i)/\mathbb{Q}$
No vamos a hacer el detalle aquí , pero tenemos que si usamos la base de $latex \mathbb{Q}(i)/\mathbb{Q}$ dada por $latex \lbrace 1,i \rbrace$ tenemos que para $latex \alpha=a+bi$ la matriz de la multiplicación por $latex \alpha$
$latex \mu_{\alpha}:\mathbb{Q}(i) \rightarrow \mathbb{Q}$
$latex z \mapsto \alpha z$
Por lo que las columnas generadas por $latex \mu_\alpha(1)=a+bi$ y $latex \mu_\alpha(i)=-b+ai$
por lo que
$latex \mu^{*}_\alpha = \begin{pmatrix}a&-b\\b & a\end{pmatrix}$
Por lo que:
$latex Tr_{\mathbb{Q}(i)/\mathbb{Q})}(\alpha)=Tr(\mu^{*}_\alpha)=2a$
Puedes notar que esta última norma, es la misma norma que utilizas en $latex \mathbb{C}$ , así es como formalmente se construyen las normas algebraicamente.
Todo listo para El teorema 90 de Hilbert y el ejemplo de la parametrización racional de la circunferencia.
Vamos a volver a enunciar el teorema y luego el corolario del ejemplo de parametrización con todos los ejemplos y lo anterior ya desarrollado.
Teorema 90 (David Hilbert)
Sea $latex L/K$ una extensión de campos cuyo grupo de Galois $latex G:=Gal(L/K)=Aut_{K}(L) =\langle \sigma \rangle$ es cíclico y si $latex x\in L$ tiene norma $latex 1$, es decir $latex N_{L/K}(x)=1$ , entonces existe $latex y\in L$ con $latex x = \frac{\sigma(y)}{y}$
Corolario 90
Considera la extensión de grado 2 $latex \mathbb{Q}(i)/\mathbb{Q}$ sabemos que es Galois y que tiene grupo $latex G:=Gal(\mathbb{Q}(i)/\mathbb{Q})=Aut_{\mathbb{Q}}(\mathbb{Q}(i)) =\langle \psi \rangle=\lbrace id, \psi \rbrace$ (donde $latex \psi$ es la conjugación como ya la construimos anteriormente), tenemos que este grupos es cíclico y de 2 elementos, si $latex \alpha=x+yi\in \mathbb{Q}(i)$ es tal que $latex N_{\mathbb{Q}(i)/\mathbb{Q})}(\alpha)=1$ esto implica que $latex N_{\mathbb{Q}(i)/\mathbb{Q})}(\alpha)=x^2 + y^2 = 1$ por lo que existe $latex \beta=c-di \in \mathbb{Q}(i)$ tal que:
$latex \alpha = \frac{\psi(\beta)}{\beta}=\frac{c+di}{c-di}=\frac{c^2-d^2}{c^2+d^2}+i\frac{2cd}{c^2+d^2}$
Por lo que $latex (\frac{c^2-d^2}{c^2+d^2}, \frac{2cd}{c^2+d^2} )\in \mathbb{Q}\times\mathbb{Q}$ es la caracterización de los puntos de norma 1 (circulo en este caso) , usando teoría de Galois.
Puedes verificar que $latex \Big(\frac{c^2-d^2}{c^2+d^2}\Big)^2 + \Big(\frac{2cd}{c^2+d^2} \Big)^2 = 1$ por lo que si $latex c=1$ obtenemos la misma ecuación de parametrización que construimos anteriormente dada por $latex \Big(\frac{1-t^2}{1+t^2},\frac{2t}{1+t^2}\Big)$
Conclusión
El álgebra y la geometría son prácticamente lo mismo, un razonamiento puramente geométrico tiene respuesta algebraica,, de eso se encargó Alexander Grothendieck de formalizar, vimos que con teoría de Galois podemos llegar al mismo resultado geométrico.
No me dio tiempo de demostrar el teorema 90, pero tal vez pronto lo haga, no es tan difícil teniendo más herramientas a la mano que sólo para el que tenga curiosidad le podrá ser útil.
Eduardo Ruiz Duarte (beck)
twitter: @toorandom