Harald Helfgott decidió probar la conjetura de Goldbach débil (todo impar mayor que 5 es suma de 3 primos) hace un par de años usando teorema de Convolución, esto es algo muy de teoría de análisis complejo y real, y yo no me imaginaría que la solución fuera por aquí, el teorema de la convolución generalmente se usa en el contexto de señales y Análisis de Fourier, en otro momento lo expondré aquí, la explicación sencilla de Helfgott y su solución aquí.
Yo no soy experto en Fourier, pero lo he usado para varios proyectos y me interesa mucho, les expongo aquí una manera intuitiva de entender la transformada de Fourier discreta.
La Transformada de Fourier trasforma una función periódica en otra función en el espacio de frecuencia, es decir, busca otra representación de la función en términos de combinaciones lineales de otras funciones, en este caso senos y cosenos, como algunos sabrán, toda función se puede aproximar por senos y cosenos por partes, estos coeficientes de senos y cosenos que arman la función original son la información de la transformada de Fourier de una función $latex f$.
$latex \hat{f}(\psi)=\int_{-\infty}^{+\infty}f(t)e^{-2\pi it\psi}dt$
donde su inversa está dada por
$latex f(t)=\int_{-\infty}^{+\infty}\hat{f}(\psi)e^{2\pi i\psi t}d\psi$
Donde $latex t$ es el tiempo y $latex f(t)$ es el valor de la señal en el tiempo $latex t$, $latex e^{2\pi i t}=cos(2\pi t)+isen(2\pi t)$ y $latex \psi$ es el valor de frecuencia.
La teoría aquí es muy bonita, pero también muy complicada, así que nos adentraremos en la parte discreta
Transformada de Fourier discreta.
La transformada de Fourier discreta (TFD) es un funcional (una función de funciones) que toma como argumento una función $latex f$ que es una señal en el tiempo y te regresa otra función $latex \hat{f}$ que contiene la información de la frecuencia en la señal original.
Para términos prácticos, una señal será sólo una sucesión de números, por ejemplo:
$latex \tilde{f}=\lbrace 1.9, -3.1, 12.3,4.8,22.9,-13.2, 11.8,4.8,-0.3 \rbrace$
Dónde $latex \tilde{f}(n)$ es el valor $latex n-$ésimo comenzando por el $latex 0$, $latex \tilde{f}(0)=1.9$
Le pongo tilde porque queremos trabajar con otra versión de esta señal que ahora explico.
Señales de promedio cero
Queremos comparar señales, para ello necesitamos trabajar con las señales "normalizadas" , en el sentido que si vamos a correlacionar $latex f$ con $latex g$ , una correlación "0" nos indique que son totalmente diferentes, para esto, sólo basta con trabajar con las señales "centradas" en su promedio y basta con restar a cada coeficiente el promedio de la señal en el intervalo de tiempo, si repitiéramos esto en la señal verían que el promedio de la señal ya sería 0 y no habría nada que restar, por eso le llamo "normalización" , en el caso del ejemplo, vemos que el promedio es $latex 4.6$ por lo que la nueva señal quedaría.
$latex f=\lbrace -2.7,-7.7,7.7,.2,18.3,-17.8,7.2,.2,-4.9 \rbrace$
La cual tiene promedio 0.
Correlación entre dos señales
Ahora, ¿cómo comparo dos señales normalizadas $latex f$ y $latex g$?
La manera más usual para señales discretas de tamaño $latex N$:
$latex \displaystyle \sum_{i=0}^N {f(i)g(i)}$
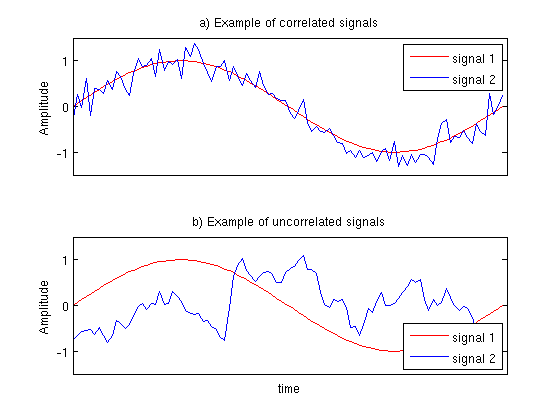
Si se fijan, gracias a la normalización tenemos las señales centradas en su promedio, por lo que si esta suma da 0 nos indicaría que no se parecen nada, ya que si $latex f(i)g(i)\geq 0$ es porque ambos valores tienen el mismo signo $latex f(i)g(i)\leq 0$ nos indicaría que difieren en signo y son "muy diferentes" , las sumas se van a ir acumulando positivamente si no hay estos cambios de signo, por lo que indica que entre más grande sea el número de la suma, más grande es la correlación siendo el máximo de correlación la suma de cuadrados de cada señal, si es un número muy grande negativo indicará que están inversamente correlacionadas (no se cancelan con los positivos) , y si es 0 , es porque las correlaciones siempre se "matan" entre negativas y positivas (no hay correlación).
Aquí dejo como se ven dos señales correlacionadas y no correlacionadas.
Para que esta medida tenga sentido, recuerden que tienen que normalizar ambas señales.
Ahora, entonces, si recuerdan, la transformada de Fourier, se multiplica la función por una exponencial compleja, es decir, están correlacionando la función con una exponencial compleja que al final son senos y cosenos, es decir... están comparando la función con senos y cosenos, y viendo qué tanto se parecen en cierto tiempo $latex t$.
La transformada para tiempo discreto $latex n$ de Fourier para una señal $latex f$ de $latex N$ valores en el tiempo se define como:
$latex F(k):=\displaystyle \sum_{n=0}^{N-1} {f(n)e^{{-2\pi i kn}/N}}$ donde $latex k\in \lbrace 0,...,N-1\rbrace$
Para cada $latex k$ obtenemos un coeficiente de Fourier, hasta ahora... creo que vamos bien, no es difícil en términos prácticos, pero ... qué es correlacionar con la exponencial compleja esa? , se ve feo y raro, pero no, recuerden que.
$latex e^{-i\theta} = cos(\theta)-isen(\theta)$
Entonces realmente tenemos que:
$latex F(k):=\displaystyle \sum_{n=0}^{N-1} {f(n)(cos({2\pi kn}/N) - i sen({2\pi kn}/N))$
$latex F(k):=\displaystyle \sum_{n=0}^{N-1} {f(n)cos({2\pi kn}/N)}-i\displaystyle \sum_{n=0}^{N-1} {f(n)sen({2\pi kn}/N)}$
Tenemos que para $latex k$ hay una función diferente.
El juego de signos es por las propiedades de paridad del seno y coseno.
Entonces lo que tenemos aquí es que la transformada de fourier realmente guarda la información en senos y cosenos que es lo que dijimos al principio (para eso se usa la exponencial) , es decir correlaciones con ambos tipos de sinusoides, y el usar la parte compleja, tiene un significado tan simple, como el hecho de hacer "linealmente independientes" a las correlaciones, ya que al final lo que nos interesará será el número real que multiplica a la parte imaginario, y no per sé la $latex i$ de análisis complejo (al menos no en este caso).
¿De qué nos sirve?
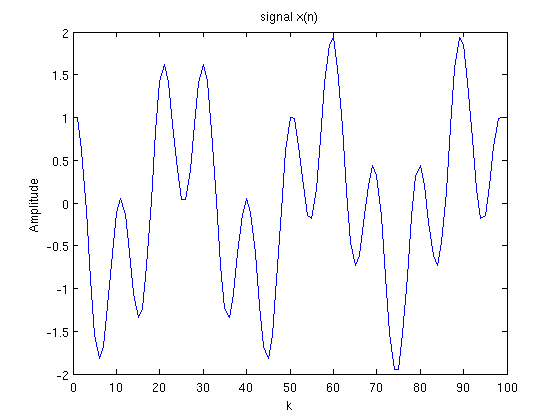
Veamos un ejemplo, supongamos que tenemos la siguiente señal $latex x(n)$ con 100 sampleos de tiempo, es decir $latex N=100$
En este caso los coeficientes para cada seno y coseno definido por $latex k$ los denotaremos como $latex X(k)$, es decir.
$latex X(k)=\displaystyle \sum_{n=0}^{N-1} {x(n)cos({2\pi kn}/N)}-i\displaystyle \sum_{n=0}^{N-1} {x(n)sen({2\pi kn}/N)}$
Para $latex k=0$ tenemos que $latex \displaystyle \sum_{i=0}^{N-1}x(n)$
Es decir solo es la suma de los valores de la señal ($latex sen(0)=0$ , $latex cos(0)=1$)
Por lo que $latex X(0)\cong 0$ ya que la señal está normalizada y tiene promedio 0.
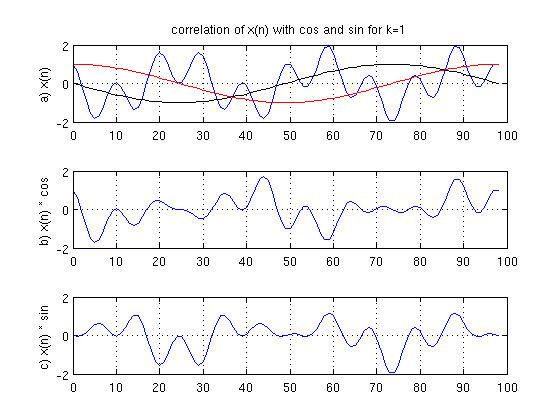
Para $latex k=1$ tenemos la siguiente información de cada sumando de la serie la transformada de fourier.
Como pueden ver en la gráfica b) y c) que la $latex X(1)=1+0i$ , es decir, no se parece nada la señal $latex x(n)$ en azul a la negra y roja tanto en seno como en coseno, pueden ver en b) , sin ser muy rigurosos en la siguiente oración: "la mitad de la señal está arriba del 0, y la otra mitad abajo" por lo que la correlación dará 0, lo mismo con c), también se cancela al sumarse sus valores. es decir, no se parecen (recuerden que b, respectivamente c) es la parte (real respectivamente compleja) de $latex X(1)$.
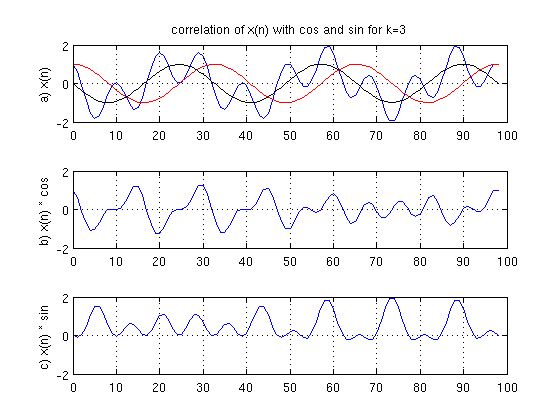
Ahora, veamos que pasa en $latex k=3$
Aquí vemos en $latex k=3$ que el seno con la señal en c) tiene gran parte positiva, y poco negativo...
por lo que la correlación nos indicará que es grande (no se cancela con negativos en la función original) y si ven en a) , pueden ver que el seno en negro en esa $latex k$ "asemeja" a la función $latex x(n)$ mientras que el coseno realmente no se parece en nada, nunca coincide con $latex x(n)$... y de hecho $latex X(3)=0+49i$.
Realmente lo que estamos buscando aquí en la transformada de Fourier, es cuando una senoidal se parece a la función original... y qué creen? , ya la encontramos,
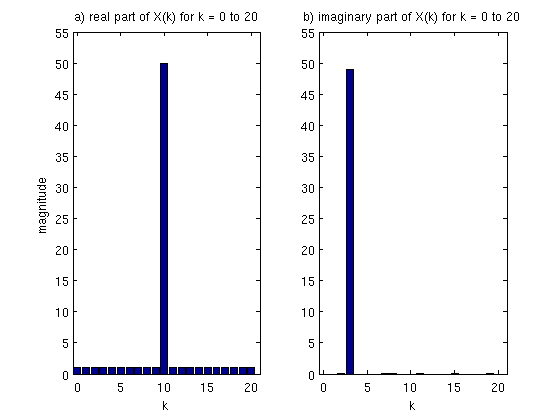
La gráfica de esta transformada de fourier se ve así para $latex k=1...20$
Como pueden ver, la transformada de Fourier, nos dice que $latex X(10)$ en el coseno se parece mucho a la función $latex x(n)$ y en $latex k=3$ tenemos que $latex X(3)$ en la parte imaginaria el seno se parece mucho a la función original, es decir hay correlación alta por ejemplo en el coseno con $latex cos(\pi t/5)$.
Pero bueno Si quiere ver todo de golpe, sin importarles si es seno y coseno (al final ambas funciones son la misma solamente recorridas) , pueden calcular su densidad espectral para cada valor $latex k$ la cual les dirá si hay sinusoides presentes en la señal la cual se define como
$latex DS_{k}(x)=\mathfrak{R}(X(k))^2 + \mathfrak{I}(X(k))^2$
Que es la suma de los cuadrados de la parte real e imaginaria de la transformada de Fourier para cada $latex k$
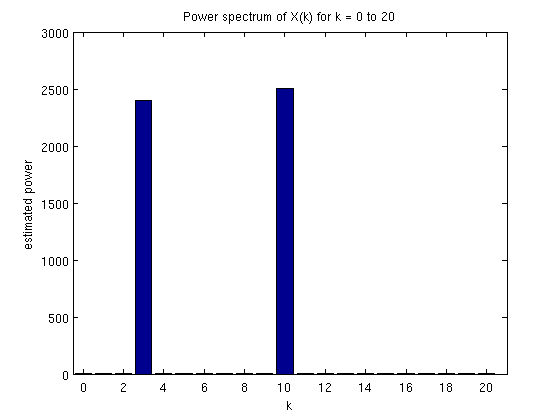
Por lo que en este ejemplo, la gráfica de la densidad espectral que ya carece de parte imaginaria, junta toda la información (aunque se pierde de qué tipo de sinodal viene, pero esto es fácil deducirlo)
Aquí pueden ver perfectamente que en $latex k=3$ y en $latex k=10$ existen sinusoides interesantes muy correlacionadas con la señal,
Mucho se habla de Frecuencia, para esto, lo más popular es usar Hz , es decir "cosas que suceden en un segundo" , y para transformar la $latex k$ en Hz , basta decidir "cada cuanto sucede un suceso" a este número llamale $latex r$ , uso $latex r$ porque es de "sampling rate" , y tenemos que en Hz, la frecuencia es $latex \xi=kr/N$ donde $latex N$ es el número de samples, o el número de valores en tu tiempo discreto, entonces ya pueden sustituir la $latex k$ por la frecuencia $latex \xi$.
Espero les haya servido como a mi, las imágenes las saqué de este sitio
Aquí les dejo del mismo sitio los valores de la señal $latex x[n]$ en el ejemplo.
1.000000, 0.616019, -0.074742, -0.867709, -1.513756, -1.814072, -1.695685, -1.238285, -0.641981, -0.148568, 0.052986, -0.099981, -0.519991, -1.004504, -1.316210, -1.277204, -0.840320, -0.109751, 0.697148, 1.332076, 1.610114, 1.479484, 1.039674, 0.500934, 0.100986, 0.011428, 0.270337, 0.767317, 1.286847, 1.593006, 1.522570, 1.050172, 0.300089, -0.500000, -1.105360, -1.347092, -1.195502, -0.769329, -0.287350, 0.018736, -0.003863, -0.368315, -0.942240, -1.498921, -1.805718, -1.715243, -1.223769, -0.474092, 0.298324, 0.855015, 1.045127, 0.861789, 0.442361, 0.012549, -0.203743, -0.073667, 0.391081, 1.037403, 1.629420, 1.939760, 1.838000, 1.341801, 0.610829, -0.114220, -0.603767, -0.726857, -0.500000, -0.078413, 0.306847, 0.441288, 0.212848, -0.342305, -1.051947, -1.673286, -1.986306, -1.878657, -1.389067, -0.692377, -0.032016, 0.373796, 0.415623, 0.133682, -0.299863, -0.650208, -0.713739, -0.399757, 0.231814, 0.991509, 1.632070, 1.942987, 1.831075, 1.355754, 0.705338, 0.123579, -0.184921, -0.133598, 0.213573, 0.668583, 0.994522, 1.000000
Eduardo Ruíz Duarte (beck)
twitter: @toorandom
1 comment:
a mi re resulta mas correcto los niveles X(k) con Real = (x(n)*COS(2*pi()*k*n/128))/64
para N=128 e imaginario (x(n)*SEN(2*PI()*k*n/128))/32
Post a Comment