Teorema de Riemann-Roch y divisores en criptografía, (Parte 2: Espacio proyectivo)

Como vimos anteriormente, lo que queremos es exprimir las propiedades de una curva algebraica a través de la geometría algebraica, en este caso de una curva elíptica o hiperelíptica.

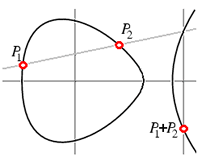
Como lo mencioné al principio del post anterior, el grupo de una curva elíptica está fundamentado de manera "cochina" por (algunos) computólogos que implementan criptografía por el teorema de Bézout.

Siempre al definir una curva elíptica se define en su propiedad de grupo que un punto $latex (x,y)$ en la curva elíptica o hiperelíptica tiene como inverso a el punto $latex (x,-y)$ lo cual sucede al proyectarlo con un punto mágico que está en el infinito, esto es porque la curva elíptica realmente no vive en $latex \mathbb{R}^2$ como todos creen, realmente vive en otro espacio que es el que trataremos de explicar aquí, vive realmente en $latex \mathbb{P}^2_{\mathbb{C}}$, pronto veremos el por qué se les llama elípticas a través de otro nuevo espacio $latex \mathbb{C}/\Lambda$ y una función llamada $latex \wp$ de Weierstrass, pero eso aún está lejos de este post.

La respuesta elegante y limpia en vez de usar Bézout para justificar la estructura de grupo de una curva elíptica o hiperelíptica está a través del teorema de Riemann-Roch el cual trataremos de comprender a grandes rasgos, no olvides checar tu literatura

El teorema de Riemann-Roch une las propiedades algebraicas y topológicas de una curva, vamos a explorarlo un poco, aunque en esta primera parte del post definiremos primero lo que es el espacio proyectivo y algunas propiedades a través de ejemplos usando topología.

Como lo mencioné, vamos a hablar ahora del espacio proyectivo $latex \mathbb{P}^{n}_{\mathbb{K}}$, en el post anterior trabajamos en el espacio afín $latex \mathbb{A}^{n}_{\mathbb{K}}$ y definimos el campo de funciones, el cual jugará un papel imporante en Riemann-Roch

Recomiendo leer al menos la página de Wikipedia de geometría proyectiva así como el artículo del plano complejo proyectivo , aquí daré cierta intuición, ejemplos, definiciones y construcciones, para no dejar ese hueco.

Sea $latex V$ un espacio vectorial de dimensión finita sobre un campo $latex \mathbb{K}$ (de hecho para nuestros propósitos el espacio que tomaremos será $latex V=\mathbb{C}^2$) y considera la siguiente relación de equivalencia entre los vectores  $latex V\setminus \lbrace 0 \rbrace$:

$latex u\sim v \Leftrightarrow \exists \lambda \in \mathbb{K}^{*} \mid u=\lambda v$

Es decir, estamos diciendo que dos vectores $latex u$ y $latex v$ estarán en la misma partición (están relacionados) sí y sólo sí están en la misma linea que pasa por el origen, es decir, este espacio consta de todas las lineas que salen del origen bajo esta relación, con un ombligo, recuerda que quitamos al 0

Por lo que tenemos que si nuestro espacio vectorial  $latex V=\mathbb{C}^2$
$latex \mathbb{P}(V):=V\setminus \lbrace 0 \rbrace / \sim$

y para reducir notación:

$latex \mathbb{P}^{n}_{\mathbb{C}}:=\mathbb{P}(\mathbb{C}^{n+1})$

Por lo que a nosotros nos interesará trabajar en:

$latex \mathbb{P}^{2}_{\mathbb{C}}$

El cual es el plano proyectivo complejo.

Esta geometría realmente nace de la perspectiva a la hora de pintar un paisaje y quieres poder mostrar el horizonte en tu obra a pesar de que éste esté en el infinito.

De hecho, los puntos de $latex \mathbb{P}^{2}_{\mathbb{C}}$ son denotados como $latex [a:b:c]$

Ejemplo:

Como a mucha banda matemática y a mi, nos gustan los ejemplos para poder entender los conceptos abstractos, afortunadamente aquí sí hay algo en lo que todo el mundo es familiar.

Vamos a ver cómo se ve $latex \mathbb{P}^{1}_{\mathbb{R}}$, de hecho vamos a demostrar que este espacio es realmente homeomorfo al círculo $latex \mathbb{S}^1$

Este espacio se le llama linea proyectiva real y nace de considerar la relación de equivalencia mencionada inicialmente sobre $latex \mathbb{R}^2$.

Más formal:

Si $latex x,y\in \mathbb{R}^2$, tenemos que $latex x\sim y \Leftrightarrow x=\lambda y$ con $latex \lambda \in \mathbb{R}$ y:

$latex \mathbb{P}^{1}_{\mathbb{R}}=\mathbb{R}^2\setminus \lbrace 0 \rbrace / \sim$

Vamos a usar topología aquí para demostrar que $latex \mathbb{S}^1$ y $latex \mathbb{P}^{1}_{\mathbb{R}}$ son homeomorfos, de hecho la topología cociente aunque supongo que hay caminos tal vez más directos.

Consideremos:

$latex \psi:\mathbb{R}^2 \setminus \lbrace 0 \rbrace \rightarrow \mathbb{P}^1_{\mathbb{R}}$
$latex (x,y) \mapsto [x:y]$

Ahora, vamos a restringir esto a $latex \mathbb{S}^1$

es decir $latex \hat\psi = \psi\mid_{\mathbb{S}^1}$ por lo que tenemos que en $latex \hat\psi :\mathbb{S}^1 \rightarrow \mathbb{P}^1_{\mathbb{R}}$  $latex \hat\psi(x,y)=\hat\psi(-x,-y)$ es decir, a cada punto del círculo bajo la relación $latex \sim$ se reduce en la restricción al círculo a una relación más simple que le llamaremos $latex \hat\sim$ la cual definimos como $latex a,b\in \mathbb{S}^1$ entonces $latex a\hat\sim b\Leftrightarrow a=-b$

Es decir, la relación restringida al círculo nos dice que las antípodas están en la misma clase de equivalencia.

Entonces lo que basta demostrar es que $latex \tilde\psi:\mathbb{S}^1/\hat\sim \rightarrow \mathbb{S}^1$
es un homeomorfismo.

Consideremos el mapeo:

$latex \phi:\mathbb{S}^1 \rightarrow \mathbb{S}^1$

$latex (x,y) \mapsto (x^{2} - y^{2},2xy)$

Este mapeo está inspirado en $latex z\mapsto z^2$ en $latex \mathbb{C}$ pero viéndolo en $latex \mathbb{R}^2$ y restringido a $latex \mathbb{S}^1 \subset \mathbb{R}^2$

Este mapeo $latex \phi$ claramente es continuo y suprayectivo y $latex \phi$ pasa por el cociente bajo $latex \hat\sim$ o sea, respeta la relación de equivalencia $latex \hat\sim$ ya que si $latex z\in\mathbb{S}^1$ tenemos que $latex \phi(z)=\phi(-z) \Rightarrow z\hat\sim -z$

Usando la propiedad universal de la topología cociente con esta $latex \phi$ tenemos que $latex \tilde\psi:\mathbb{S}^1/\hat\sim \rightarrow \mathbb{S}^1$ es un homeomorfismo y es único.

Por lo que:

$latex \mathbb{P}^{1}_{\mathbb{R}}=\mathbb{R}^2\setminus \lbrace 0 \rbrace / \sim \cong \mathbb{S}^1$


Más ejemplos usuales existen , por ejemplo si nos tomamos $latex \mathbb{C}$ en vez de $latex \mathbb{R}$ ustedes pueden demostrar que la recta proyectiva compleja:

$latex \mathbb{P}^{1}_{\mathbb{C}} \cong \hat{\mathbb{C}}:=\mathbb{C}\cup \lbrace \infty \rbrace$

La cual es la esfera de Riemann, éste es un ejemplo fundamental en análisis complejo y geometría algebraica por ser una superficie de Riemann compacta, esto último es relevante ya que nos permite verla como una curva proyectiva algebraica.

Los espacios proyectivos complejos son una herramienta muy poderosa, ya que al agregar este punto $latex \infty$ en ciertos casos se puede definir la división por 0 haciendo que por ejemplo cualquier función racional meromorfa en los complejos sea extendida a una función continua sobre la la recta proyectiva compleja, mapeando sus polos al infinito y conservando continuidad.

En los espacios proyectivos suceden cosas interesantes, por ejemplo veremos que por la naturaleza del espacio en función de su relación de equivalencia, las ecuaciones algebraicas dentro de nuestro espacio proyectivo deberán ser homogéneas, o que existen un puntos que no están en el espacio vectorial en correspondencia con el proyectivo o que si definimos dos rectas paralelas en el espacio vectorial y lo transladamos al espacio proyectivo sí se intersectarán, de hecho TODAS las rectas del espacio proyectivo se intersectan en un punto 

Regresando a la analogía de las obras de pintura de paisajes, imagina ¿cómo pintarías la foto de unas vías del tren vistas de frente?, si observas bien las vías, éstas, pareciera que se intersectan en el horizonte.

Para terminar esto veamos lo que mencioné en negritas el penúltimo parrafo a éste.

Consideremos las soluciones (el conjunto de ceros) de un polinomio definido con sus variables en $latex \mathbb{P}^{n}_{\mathbb{K}}$ es decir, un punto en general sería con $latex n+1$ variables , $latex P=[x_0:...x_n]\in \mathbb{P}^{n}_{\mathbb{K}}$, estos puntos por como está definido el espacio proyectivo, están determinados por la multiplicación por un escalar $latex \lambda$, el cual da la relación de equivalencia, por lo que un polinomio con variables proyectivas deberán considerar esa restricción a la hora de considerar sus soluciones, estos polinomios se les llama homogéneos

Definición (polinomio homogéneo): Un polinomio:

$latex f(x_0,x_1,...,x_n) = \displaystyle \sum { a_{\eta_0...\eta_n}}x_{0}^{\eta_0}...x_{n}^{\eta_n}$

Se dice homogeneo de grado $latex d$ si TODOS sus monomios tienen el mismo grado $latex d=\sum_{i=0}^{n} \eta_i$

Por lo que si $latex f$ es homogéneo de grado $latex d$ entonces:

$latex f(\lambda x_0, ..., \lambda x_n)=\lambda^d f(x_0,...,x_n)$

Con esto tenemos que los polinomios homogéneos están bien definidos en el espacio proyectivo.

Ahora, lo que nos resta ver es una propiedad interesante, dos lineas siempre se intersectan en el plano proyectivo, y para esto lo que haremos un ejemplo, será transformar polinomios en dos variables complejas $latex \mathbb{C}^2$ a polinomios en $latex \mathbb{P}^2_{\mathbb{C}}$ a través de un proceso que se llama "homogenización" , y lo haremos con dos lineas paralelas, y veremos como es la intersección de sus imágenes.

La siguiente definición es para construir un polinomio cualquiera, a un polinomio homogéneo , es decir con monomios del mismo grado, esta operación es invertible.

Definición (homogeinización): Sea $latex p(x,y) \in \mathbb{C}[x,y]$, el polinomio correspondiente en $latex \mathbb{P}^2_{\mathbb{C}}$ es:

$latex p(x,y,z)=z^{n}p(\frac{x}{z},\frac{y}{z})$

Es fácil ver que el polinomio resultante de este proceso es realmente homogéneo.

Ejemplo (intersección de las imágenes bajo homogenización de dos rectas afines):

Sean
$latex x+y=2$
$latex x+y=3$

dos rectas definidas en $latex \mathbb{C}^2$

claramente son paralelas, homogeneizando tenemos que

$latex x+y=2z$
$latex x+y=3z$

por lo que tenemos que $latex [a:-a:0] \in \mathbb{P}^2_{\mathbb{C}}$ está en la linea al infinito y es solución de ambas ecuaciones,

nota que $latex [0:0:0]$ también es solución, pero éste punto no está definido en el espacio proyectivo por construcción.

Otro ejemplo serían dos circunferencias de radio distinto:


$latex x^2 + y^2 = 1$
$latex x^2 + y^2 = 2$

Claramente no se intersectan en el espacio afín complejo

Homogeneizando, tenemos que

$latex x^2 + y^2 -1 \mapsto z^2\Big ( \frac{x^2}{z^2}+\frac{y^2}{z^2}-1\Big )=x^2+y^2-z^2$

Similarmente con el otro polinomio, por lo que tenemos que intersectar en $latex \mathbb{P}^2_{\mathbb{C}}$

$latex x^2+y^2-z^2$   y   $latex x^2+y^2-2z^2$

y tenemos que todos los puntos de la forma $latex \lambda(\pm 1,\pm i,0)$ son soluciones, y si $latex \lambda \neq 0$

tenemos que $latex [\pm 1:\pm i:0]\in \mathbb{P}^2_{\mathbb{C}}$ es un punto en la linea al infinito que intersecta a ambas circunferencias proyectivas de distinto radio.

La relación con curvas elípticas será que éstas realmente hay que proyectivizarlas (homogeneizarlas) y al trabajar con ellas en criptografía es viéndolas en el espacio proyectivo, es decir para que todo funcione como queremos necesitamos la cerradura proyectiva, mas no el hecho de usar un punto cualquiera para darle estructura de grupo.


Con esto, y el post anterior estamos listos para la siguiente parte que será el teorema de Riemann-Roch


Eduardo Ruiz Duarte (beck)
twitter: @toorandom

Teorema de Riemann-Roch y divisores en criptografía (Parte 1: campos de funciones y gavillas sobre variedades)

En criptografía muchos han visto que se estudian las curvas elípticas y menos frecuentemente las curvas hiperelípticas, algunos recordarán la estructura de grupo que se le da a una curva elíptica $latex C$ con la usual regla de intersección de una recta con la curva haciendo uso abusivo del teorema de Bézout para fundamentar la estructura de grupo que hay en sus puntos, que más formalmente, es la estructura de grupo que hay en las clases de divisores formados por las sumas formales de ideales máximos de todos los subanillos del campo de funciones de $latex \mathbb{K}(C)$, este grupo es el grupo de Picard de orden 0 de la curva $latex C$ que es:

 $latex Pic^0(C) = Div^0(C)/Prin(C) \cong \mathbb{J}(C)$.

Esta manera de ver las cosas NO es para complicar lo ya existente, sino es con propósitos de poder exprimir más la teoría que lo respalda para poder investigarlo mejor y generalizarlo a otras curvas no elípticas.

La estructura de grupo de manera inocente o usual se puede ver en muchos textos pobres en matemáticas pero tal vez ricos en aplicaciones criptográficas como esto:

El propósito de este post será el poder resumirte la teoría que hay detrás.


Comencemos con unas definiciones, voy a suponer que quien me lee está familiarizado con la topología de Zariski la cual está definida por los conjuntos algebraicos como cerrados, de hecho estas definiciones son las interesantes para la topología de Zariski, y con esto pueden demostrar fácilmente las propiedades de espacio topológico.

Definición (ceros):
Sea $latex A:= \mathbb{K}[x_1,...,x_n]$ el anillo de polinomios en $latex n$ variables sobre el campo algebraicamente cerrado $latex \mathbb{K}$ y $latex J \subset \mathbb{K}[x_1,...,x_n]$ un ideal, entonces definimos el conjunto de ceros del ideal $latex J$ como:

$latex V(J):=\lbrace P\in \mathbb{A}^{n}_{\mathbb{K}} \mid f(P)=0$     $latex \forall f\in J\rbrace$


Definición (variedad afín): Un subconjunto $latex X\subset \mathbb{A}^n_{\mathbb{K}}$ es un conjunto algebraico (variedad afín) en el espacio afín $latex \mathbb{A}^n_{\mathbb{K}}$ si existe un $latex T\subset \mathbb{K}[x_1,...,x_n]$ tal que:

$latex X=V(T)$

Decimos que $latex X$ es un cerrado de Zariski, en la topología dada a  $latex \mathbb{A}^n_{\mathbb{K}}$.

Veámos primero lo que es el anillo de coordenadas de una variedad.

Definición (función polinomial en la variedad V): Una función polinomial es un mapeo $latex f:V \rightarrow \mathbb{K}$ tal que existe un $latex F\in \mathbb{K}[x_1,...,x_n]$ con $latex f(P)=F(P)$  $latex \forall P\in V$

Este polinomio $latex F$ no está únicamente determinado por los valores que toma en $latex V$ o sea si tenemos $latex F,G\in \mathbb{K}[x_1,...,x_n]$:


$latex F\mid_{V}=G\mid_{V} \Leftrightarrow (F-G)\mid_{V}=0 \Leftrightarrow F-G\in I(V)$

Donde:

$latex I(V):=\lbrace f\in \mathbb{K}[x_1,...,x_n] \mid f(P)=0$    $latex \forall P\in V\rbrace$



Esta definición de función polinomial y su relación de igualdad con otros polinomios, huele a una relación de equivalencia, por lo que vamos a suponer que lo es y se deja a quien lee para que lo demuestre y tenemos que:

Denotaremos ahora a $latex V$ como el conjunto algebraico $latex V(I)$ donde $latex I$ es ideal de $latex \mathbb{K}[x_1,...,x_n]$

Definición (anillo de coordenadas de una variedad): Un anillo de coordenadas de una variedad $latex V$ es:

$latex \mathbb{K}[V]:=\mathbb{K}[x_1,...,x_n]/I(V)$

Este anillo sabemos que es un dominio entero si $latex I(V)$ es un ideal primo, y esto naturalmente sucede si $latex V$ es irreducible , es decir no es union de otros cerrados de zariski


De lo anterior sobre funciones polinomiales y la última definición se puede demostrar que:

$latex K[V]=\lbrace f \mid f:V\rightarrow \mathbb{K}$ es una función polinomial $latex \rbrace$

Cabe notar que se le llama anillo de coordenadas porque las funciones que te dan la i-ésima coordenada de los elementos de $latex V$, $latex x_i$ son las generadoras de $latex \mathbb{K}[V]$

Es fácil ver que $latex \mathbb{K}[ \mathbb{A}^n_{\mathbb{K}}]=\mathbb{K}[x_1,...,x_n]$ y que el anillo $latex \mathbb{K}[V]$ juega el papel para $latex V$ como $latex \mathbb{K}[x_1,...,x_n]$ para $latex \mathbb{A}^n_{\mathbb{K}}$

Observaciónes sobre lo anterior con respecto a la topología de Zariski en $latex \mathbb{A}^n_{\mathbb{K}}$.

• Los ideales primos de $latex \mathbb{K}[V]$ están en correspondencia 1:1 con irreducibles $latex W\subset V$
• Los ideales máximos de  $latex \mathbb{K}[V]$ están en correspondencia 1:1 con los puntos de $latex V$
• Los ideales radicales de $latex \mathbb{K}[V]$ están en correspondencia 1:1 con los cerrados $latex W\subset V$

Definición (campo de funciones de V): El campo de funciones de $latex V$ es el campo de fracciones de $latex \mathbb{K}[V]$ y es denotado por $latex \mathbb{K}(V)$, las $latex f\in \mathbb{K}(V)$ se llaman funciones racionales sobre $latex V$

Definición (función regular en P): Una función $latex f\in \mathbb{K}(V)$ y $latex P\in V$ se dice que es regular en $latex P$ si $latex f=\frac{g}{h}$ con $latex h(P)\neq 0$, y definimos:

$latex dom(f):=\lbrace P\in V \mid f$ es regular en $latex P\rbrace$

Proposición: El conjunto:

$latex V_f:=\lbrace P\in V\mid f(P)\neq 0\rbrace$

es un abierto de $latex V$


Teorema: 

• $latex dom(f)$ es abierto y denso en $latex V$
• $latex dom(f)=V\Leftrightarrow f\in \mathbb{K}[V]$
• $latex V_g\subset dom(f) \Leftrightarrow f\in \mathbb{K}[V][1/g]$

Ahora, entraremos a un concepto central, para poder analizar una variedad localmente... para esto sabemos que un anillo local sólo tienen un ideal máximo, y tenemos que la siguiente definición

Definición (anillo de funciones regulares): El anillo de funciones regulares de $latex V$ localizado en el punto $latex P\in V$ es:

$latex O_{V,P}:=\lbrace f\in \mathbb{K}(V)\mid f$ es regular en $latex P\rbrace$

Es fácil demostrar que esto es en efecto un subanillo de $latex  \mathbb{K}(V)$ y que su único ideal máximo no deberá tener unidades por lo que su ideal máximo es:

$latex m_{P}:=\lbrace f/g \in \mathbb{K}(V)\mid f(P)=0, g(P)\neq 0 \rbrace$

Ahora vamos a la últma parte de este blog donde discutiremos la estructura de gavilla de una variedad

Estructura de gavilla de una variedad

Tenemos que el anillo $latex O_{V,P}$ es local y es un subanillo de $latex \mathbb{K}(V)$ y su ideal máximo es $latex m_{P}$, es fácil relacionar a $latex O_{V,P}$ con $latex \mathbb{K}[V]$ ya que con localización puedes demostrar que:

$latex \hat{m}_P=\lbrace f\in \mathbb{K}[V]\mid f(P)=0\rbrace=I(\lbrace P \rbrace)+I(V)\subset \mathbb{K}[V]$

Es máximo y:

$latex O_{V,P}=\mathbb{K}[V]_{\hat{m}_P}$


Es decir que $latex O_{V,P}$ es la localización del anillo de coordenadas de $latex V$ en el ideal máximo $latex \hat{m}_P$

Ahora vamos a definir el concepto final:

Definición-Teorema (estructura de gavilla en $latex O_{V}(U)$, germen y fibra ): Para todo abierto $latex U \subset V$ tenemos:

$latex O(U):=O_{V}(U):=\lbrace f\in \mathbb{K}(V) \mid f$ es regular en $latex U \rbrace$

Es una $latex \mathbb{K}-$álgebra con $latex O_{V}(\emptyset):=\lbrace 0 \rbrace$

Todos los $latex O_{V}(U)$ con $latex U\subset V$ forman una gavilla $latex O_V$ bajo la restricción de homomorfismos usual y el anillo $latex O_{V,P}$ es una fibra de la gavilla $latex O_V$  y los elementos $latex f\in O_{V,P}$ se les llama gérmenes de funciones y:

$latex O(V)=\mathbb{K}[V]$


La teoría de gavillas da una estructura rica a una variedad, en este caso , puede ser el de una curva elíptica o hiperelíptica

Saludos

Eduardo Ruiz Duarte (beck)
Twitter: @toorandom

Criptografía asimétrica combinatoria-algebraica no usual con bases de Gröbner

Siempre me ha gustado investigar estructuras algebraicas con el fin de poder ver si puedo sumergir criptografía asimétrica dura ahí, generalmente ésta basada en el problema de logaritmo discreto en curvas algebraicas; considero que es mi área favorita de trabajo y posiblemente a lo que me vaya a dedicar el resto de mi vida, pero aquí vamos a ver algo diferente que podría o no ser seguro en su implementación pero no deja de ser interesante.


Primero vamos a analizar un caso particular de un esquema de cifrado con polinomios y luego veremos cómo generalizarlo y definiendo con bases de Gröbner.

Vamos a utilizar cualquier $latex \mathbb{F}-algebra$ de tipo finito, i.e. finitamente generada, con grado de trascendencia $latex n$ veamos cómo funciona esto.

Construcción del algoritmo de cifrado:

Sea $latex \mathbb{F}$ un campo finito y $latex T=\lbrace t_{i}\rbrace_{i=1}^{n}$ un conjunto de variables.


Queremos que $latex A$ reciba un mensaje $latex m\in \mathbb{F}$ de $latex B$ cifrado.

• $latex A$ va a escoger un vector aleatorio $latex y\in \mathbb{F}^{n}$ como llave privada

• $latex A$ escoge polinomios como llave pública $latex P=\lbrace q_j \rbrace \subseteq \mathbb{F}[T]$ tal que $latex q_j(y)=0$ $latex \forall j$

         Es fácil generar polinomios con los ceros que necesitamos, por ejemplo si
         ya tenemos la llave privada $latex y$ tomas $latex q_j = \hat {q}_j - \hat{q}_j(y)$ con $latex \hat{q}_j \in \mathbb{F}[T]$.
         Lo que no es tan fácil es escogerlos seguros y álgebraicamente independientes, pero hay métodos.

•  $latex B$ quiere mandar el mensaje $latex m\in \mathbb{F}$ a $latex A$ por lo que se toma un elemento del ideal generado por la llave pública $latex P$ que es $latex (P) \subset \mathbb{F}[T]$:

   $latex p = \displaystyle \sum { h_j q_j } $

En otras palabras escoge $latex \lbrace h_j \rbrace \subset \mathbb{F}[T]$ y genera el polinomio $latex p$

• $latex B$ le manda a $latex A$ el polinomio multivariable        

$latex c=p+m$


Este esquema de cifrado funciona ya que $latex A$ va a poder obtener $latex m\in \mathbb{F}$ ya que conoce los ceros de los generadores del ideal $latex (P)\in \mathbb{F}[T]$ por lo tanto conoce los ceros de $latex p$ independientemente de los $latex \lbrace h_j \rbrace$ , por lo que usando su llave privada $latex y$ tenemos que $latex A$ puede calcular fácilmente

$latex c(y)=p(y)+m=m$


Nota que este esquema de cifrado es probabilístico y no determinístico, i.e. en cada
ocasión que se cifra $latex m$ es diferente ya que depende de los elementos del ideal de la llave pública que se tomen.

Su seguridad también depende de los ceros del conjunto algebraico generado por $latex B$, en este caso cada cero sería $latex y=(y_1,y_2,...,y_n)$ y cualquier cero en la intersección de las hipersuperficies funcionaría, su seguridad depende de la solución de sistemas de ecuaciones algebraicos no lineales de grado arbitrario , es decir, en dimensión grande y con un número grande de polinomios generadores independientes del ideal de la llave pública, es POSIBLE tener criptografía segura, digo posible porque no se ha demostrado que su solución NO sea en tiempo polinomial, pero creo que podría ser más seguro si usamos la teoría de bases de Gröbner.

Generalización:

Veamos unas definiciones que vienen de la teoría de bases de Gröbner para poder intentar una generalización, las cuales incluyen la reducción módulo otro polinomio multivariable, donde los monomios deberán estar ordenados bajo cierto orden lexicográfico.

Definición (módulo polinomio multivariable): Decimos que $latex f$ reduce a $latex h$ módulo $latex g$ parcialmente si $latex a_{i}X^{i}$ es un monomio de $latex f$ que es divisible por el término líder de $latex g$ ,$latex lt(g)$ (líder bajo el órden con el que organicemos nuestros polinomios como el lexicográfico por grado) y que sucede que:

$latex h=f-\frac{a_{i}X^{i}}{lt(g)}g$

Donde escribimos que $latex f \equiv h \bmod g$

Definición (módulo un conjunto de polinomios): Sea $latex G=\lbrace g_1,...,g_l \rbrace \subset \mathbb{F}[T]$ y sea $latex f\in \mathbb{F}[T]$, entonces decimos que $latex f$ se reduce a $latex h$ módulo $latex G$ ($latex f \equiv h \bmod G$) si tenemos la sucesión $latex h_0=f, ..., h_k=h$ tal que $latex h_j \equiv h_{j+1} \bmod g$ para algún $latex g\in G$

Definición (base de Gröbner): Sea $latex F=\lbrace g_1, ..., g_l \rbrace \subset \mathbb{F}[T]$ un conjunto finito de polinomios en $latex m=|T|$ variables e $latex I\subset \mathbb{F}[T]$ el ideal generado por $latex F$, decimos que $latex F$ es una base de Gröbner para el ideal $latex I$ si para todo $latex 0\neq f\in I$ se tiene que $latex lt(g_k)\mid lt(f)$ para algún $latex g_k\in F$


Teorema: F es una base de Gröbner para un ideal $latex I\subset \mathbb{F}[T]$ $latex \Leftrightarrow$ $latex \forall f \in I$ $latex f\equiv 0 \bmod F$

Con este último teorema nos resulta TRIVIAL el poder construir ideales aleatorios (finitos, anillos noetherianos) y su base de Gröbner asociada.

Regresando al esquema de cifrado original y rehaciéndolo con esto:

$latex A$ escoge una base de Gröbner $latex G=\lbrace g_1,...,g_l\rbrace$ de un ideal $latex I \subset \mathbb{F}[T]$, la llave privada de $latex A$ es $latex G$.

Sea $latex S\subset \mathbb{F}[T]$ el conjunto de TODOS los polinomios que no pueden ser reducidos módulo $latex G$ (ve las definiciones anteriores), este $latex S$ realmente sería el conjunto de representantes del anillo $latex \mathbb{F}[T]/I$ como ya se lo habrán imaginado, ahora supón que $latex S$ es público, aunque $latex G$ no lo sea, tenemos que todo mensaje $latex m \in \mathbb{F}$ es un elemento de $latex S$.

Un ejemplo:


 Sea $latex T=\lbrace t_1,...,t_n\rbrace$ y $latex y \in \mathbb{F}^n$ un punto secreto, $latex A$ toma como base de gröbner $latex G=\lbrace t_1-y_1, ..., t_n - y_n\rbrace$  en este caso tenemos que $latex S=\mathbb{F}[T]/(G)\cong \mathbb{F}$ es el campo de las constantes.

Ahora $latex A$ escoge un conjunto como llave pública $latex P=\lbrace q_j \rbrace \subset I=(G)$, esto es fácil ya que  podría tomar un $latex \hat{q}_j\in \mathbb{F}[T]$ arbitrario y calcular $latex q_j = \hat{q}_j - \overline{q}_j$ donde $latex \overline{q}_j \in S$ y $latex \hat{q}_j \equiv \overline{q}_j \bmod G$

Consideremos el ideal $latex J=(P)$ y $latex m\in S$, entonces $latex B$ le cifrará a $latex A$ el mensaje $latex m$ escogiendo al azar un elemento de $latex J$, ya que la llave pública de $latex A$ es $latex P$ y $latex J=(P)$:

$latex p=\displaystyle \sum h_{j}q{j} \in J$

$latex B$ le manda a $latex A$ $latex c=p+m$

$latex A$ al recibir $latex c$ sólo tendría que reducirlo módulo la base de Gröbner $latex G$ 

En este ejemplo cuando $latex G=\lbrace t_i - y_i \rbrace$ sería el caso particular que vimos en el principio.


Esta criptografía es rara y no es usada ni considerada AÚN SEGURA debido a que falta demostrar que tan dificil es el problema en términos de complejidad.


Espero les haya gustado

Eduardo Ruíz Duarte (beck)
@toorandom

Hice programa para simular evolución de organismos libre, licencia MIT, simulacion genetica con bases nitrogenadas y estructura similar a una celula

Hice un algoritmo evolutivo que la simple lectura de su código posiblemente te hará entender los fundamentos de la teoría de darwin y su selección natural, así como los fundamentos de reproducción celular y herencia es un api pero trae un demo, uso bases nitrogenadas reales complementarias y células con una estructura similar a un organismo (con respecto a su núcleo y material genético).

La reproducción se da entre los más aptos random en el universo de población con distribución uniforme bajo el producto de sus aptitudes con respecto a un gen elite.

La manera de que estos se juntan es si son más aptos, esto es para simular el elitismo biologico, podrian reproducirse otros no aptos con cierta probabilidad .

Sus hijos comparten aproximadamente la mitad de los genes de sus padres.

Las poblaciones envejecen en cada generación, dañando el ADN en cierto porcentaje de los menos aptos.


Corranlo... trae un demo y me dicen que opinan... segun yo quedo muy didactico.

Y se puede adaptar para usar genomas reales y trazar evolucion no solo de 1 gen sino de varios a la vez.

En mi programa una celula humana ocuparía aproximadamente 9gb de memoria (46 cromosomas, 30 mil genes en el ADN con 1000 pares de bases nitrogenadas)

Por lo que en el demo uso un organismo con 4 cromosomas pero pueden bajar los genomas de ECOLI que ocupan como 6 mb en mi programa y generar poblaciones para ver como evolucionan... aqui tengo uno.

http://math.co.ro/ecoli.dna

Gracias Ximena Tochtli Bouchain Pedrón
por resolverme dudas de genética y reproducción celular, ya que con sus tips y consejos esto funciona y es más realista :)

Esta aquí el leeme y el código
http://b3ck.blogspot.mx
Salu2

Eduardo Ruiz (beck)


Aquí dejo el LEEME.TXT

bevolucion-0.1.tar.gz

Copyright Nov-2013 Eduardo Ruiz Duarte (rduarte@ciencias.unam.mx)


Programa para calcular las generaciones requeridas para alcanzar la estructura de un gen definida
utilizando la estructura aproximada biologica de un organismo.

Si quieres aprender un poco de genetica basica fundamental, sigue leyendo y corre este programa

Si quieres aprender mas de la parte biologica, quien me asesoro fue Ximena Tochtli Bouchain, escribele a rhapanus@gmail.com

Si quieres saber como funciona el API , lee los prototipos y sus comentarios al final del header bevolucion.h

Si estas desesperado y te da flojera leer esto , solo compila y corre el programa que ya trae un DEMO

./compila
./bevolucion


en el ejemplo se intenta evolucionar a un gen_elite aleatorio.



COMO FUNCIONA?

Se puede definir.
numero de organismos
numero de cromosomas
numero de genes
numero de pares de bases nitrogenadas por gen
coeficiente de mutacion (cuantos pares de bases se van a modificar aleatoriamente en todos los genes... podrian no modificarse algunos genes por probabilidad)
cromosoma y gen de referencia para analizar su evolucion

QUE HAY EN EL DEMO? [ main() ]

En el main() se implementa:

 INICIO_ALGORITMO {

1. El programa genera una poblacion con genes aleatorios y un gen_elite para comparar la evolucion, cada organismo contiene en su 'ser'
  su coeficiente de adaptacion con respecto al gen_elite

  LOOP() {
2. Se organizan jerarquicamente en funcion de su adaptacion al gen_elite

3. Usando la distribucion aleatoria uniforme escogemos aleatoriamente 2 padres aptos para reproducirse (de acuerdo a su coeficiente de adaptacion)
  podrian no ser los mas aptos, pero la funcion esta probada para arrojar mayormente aptos al azar.
  para simular elitismo usual entre organismos.

4. Se reproducen y generan un hijo con cierta probabilidad de mutacion y se le integra en su 'ser' su coeficiente de adaptacion
  el ADN de el hijo contiene genes con 50% de probabilidad del padre y 50% de probabilidad de la madre

5. Se integra a la poblacion si este hijo es mas apto que el menos apto

6. Muere el menos apto

7. Envejece 1/3 de la poblacion menos adaptada de manera que se dania el ADN,  el danio es una mutacion
  de solo 1 par de bases nitrogenadas en el gen de referencia.
  Esto esta fundamentado en que el envejecimiento consiste en la creacion de proteinas menos adecuadas
  para el ciclo de vida de las celulas debido a que el ADN contiene ya informacion erronea
  (el ADN contiene las 'instrucciones' del ciclo de vida de una celula, creacion de proteinas)
  Por ejemplo los rayos UV danian el gen XPD humano que llevan a defectos en la reparacion del ADN y transcripccion.
  las personas con este danio tienen el sindrome de Cockayne, por eso aqui modelamos con 1/3 de los menos
  adaptados la mutacion en el gen de referencia.

 }
}
FIN_ALGORITMO


Cada organismo (celula) esta organizada asi:

typedef struct celula_s
{
  cromosoma cromosomas[MAX_CROMOSOMAS];
  int16_t num_cromo;
  int16_t num_genes;
  int32_t aptitud_gen_ref;
  uint64_t identidad;
  uint32_t padre, madre;
  int32_t num_hijos;
  int32_t hijos[MAX_HIJOS];
 } celula;

donde su 'identidad' esta compuesta de 64 bits
{20 bits info de padre}{20 bits info de madre}{4 bits pseudo-random}{20 bits (Padre XOR Madre) + num_hijos_padre+num_hijos_madre}


Las variables globales gGen_ref y gCromo_ref son para encontrar el gen de referencia para evolucionar, esta definida en main() y se genera aleatoriamente ej. (ATCGGCTA)


Todas las subestructuras estan organizadas jerarquicamente con los componentes biologicos del organismo simple (solo nucleo)


CROMOSOMA:
Un cromosoma tiene el ADN enrollado y tiene asociadas proteinas, especialmente histonas, aqui las podemos relacionar con el mismo indice
pero la estructura de proteinas que el cuerpo usa para unir el ADN como cromatina no se usa aun en esta implementacion aun (ni otras proteinas)

typedef struct cromosoma_s
{
adn molecula_adn;
uint64_t proteinas[MAX_GENES * MAX_NUC_GEN];
} cromosoma;

ADN:
El ADN esta seccionado por genes
typedef struct adn_s
{
gen genes[MAX_GENES];
int8_t recesivo;
} adn;

GEN:
Un Gen esta compuesto de bases nitrogenadas, y guardaremos su aptitud y tamanio de pares de bases nitrogenadas en format AT,TA,GC,CG,AU,UA
que son los pares complementarios de pirimidinas y purinas en el ADN de un organismo y en ARN (U:=Uracilo que sustituye T=Timina)

typedef struct gen_s
{
  uint8_t par_bases[MAX_NUC_GEN];
  uint16_t tamano;
  uint32_t aptitud;
} gen;


PAR DE BASES NITROGENADAS

#define Adenina     0x08
#define Citosina    0x04
#define Guanina     0x02
#define Timina      0x01
#define Uracilo     0x0f
 ADN pares complementarios
#define AT (int8_t)(Adenina<<4 imina="" p="">#define TA (int8_t)(Timina<<4 denina="" p="">#define GC (int8_t)(Guanina<<4 itosina="" p="">#define CG (int8_t)(Citosina<<4 p="" uanina=""> ARN pares complementarios
#define AU (int8_t)(Adenina<<4 p="" racilo="">#define UA (int8_t)(Uracilo<<4 denina="" p="">

Integración motívica

Existe toda una teoría motívica de integración para cada variedad compleja suave, y esto sirve para la nueva teoría de cuerdas, la teoría motívica fue introducida por Kontsevich en 1995, donde anunció una solución a la conjetura de Batyrev sobre 

dos variedades Calabi-Yau birracionalmente equivalentes tienen los mismos números de Hodge.

Esta conjetura motivó el trabajo en física teórica ya mencionado sobre teoría de cuerdas, donde se cree que el universo visto como una variedad  es localmente el producto de $latex \mathbb{R}^4$ (Minkowski) con un componente compacto (Una variedad de Calabi-Yau)

Aquí sólo resumiremos un artículo de Looijenga (Motivic Measures)  sobre como se debe interpretar la integral motívica, para poder medir volúmenes, o cualquier cosa en cualquier variedad, dimensión, et cétera.

recomiendo leer también What is motivic measure? de Hales, donde expone la aritmética motívica a detalle de J. Denef y F. Loeser, como aquí lo mencioné aquí veremos en resumen lo que es "Motivic Measures" de Looijenga.

La integración motívica toma valores en el anillo motívico $latex \mathbb{M}$ el cual a grandes rasgos tiene como elementos combinaciones $latex \mathbb{Z}$-lineales formales de variedades, con suma como la suma disjunta de variedades y multiplicación como el producto directo de éstas.

Este anillo no está ordenado.

Sea $latex \Omega \\$ una variedad compleja de dimensión $latex n \\$ y $latex \displaystyle \mathfrak{D}=\sum_{i=1}^{r}a_{i}\mathfrak{D}_{i}$ un divisor efectivo en $latex \Omega \\$ con cruces normales simples, la integral motívica del par $latex (\Omega,\mathfrak{D})$ es:

$latex \int_{J_{\infty}(\Omega)}F_{\mathfrak{D}}d_{\mu}=\displaystyle \sum_{J\subseteq \lbrace 1,...,r\rbrace} [\mathfrak{D}^{\circ}_{J}]\cdot \Big (\prod_{j\in J} \frac{\mathbb{L}-1}{\mathbb{L}^{a_{j}+1}-1}\cdot \mathbb{L}^{-n} \Big )$ 

Aquí el espacio de arcos formales de $latex \Omega \\$ es $latex J_\infty(\Omega)$ , aquí también $latex F_{\mathfrak{D}$ es una función definida en $latex J_\infty(\Omega)$, la integral motívica de $latex (\Omega, \mathfrak{D})$ es la integral de $latex F_{\mathfrak{D}$ sobre $latex J_\infty(\Omega)$ respecto a una medida $latex \mu \\$ en $latex J_\infty(\Omega)$, esta medida toma valores en $latex \mathbb{M} $

Los arcos formales $latex J_\infty(\Omega)$ están definidos fijando una variedad compleja $latex \Omega \\$ , los puntos de este espacio corresponden a "arcos formales" , imagina una curva infinitesimal centrada en un punto de $latex \Omega \\ $, eso es un punto con una dirección  tangente en ese punto, una dirección tangente de segundo orden, de tercer orden, et cétera... por eso se puede "intuir" que $latex J_\infty(\Omega)$ es un haz afín infinidimensional sobre $latex \Omega \\$.

$latex \mathbb{L}$ es la línea afín en $latex \mathbb{M}$

Espacios tangente y derivaciones

Ya vimos cómo funcionan las k-formas diferenciales y de hecho construímos con ellas el rotacional, divergencia y gradiente, vamos ahora a construir el espacio tangente, como repito, esto es con el fin de poder entender qué sucede en la topología de Zariski a la hora de definir el espacio tangente allí y usar las herramientas de geometría diferencial en geometría algebraica para el cálculo de singularidades, ahora lo haremos en $latex \mathbb{R}^n$ después esto se podrá dar el salgo a geometría algebraica para definirlo en $latex \mathbb{A}^{n}_{\mathbb{K}$ o en $latex \mathbb{P}^{n}_{\mathbb{K}$ , todo esto es para después definir orientación lo cual es un tema a mi gusto un poco complicado, pero es necesario para saber la "dirección" de la derivada y cómo se comportan los campos vectoriales.

Estoy suponiendo que el lector conoce lo que es una variedad (diferenciable) en $latex \mathbb{R}^n$, si no lo conoce, de manera rápida, una variedad de dimensión n es un espacio topológico en el cual para todo punto de éste existe un abierto al cual pertenece ese punto, y ese abierto es homeomorfo a $latex \mathbb{R}^n$, esta variedad es diferenciable si no tiene autointersecciones, picos, etcétera .

Recuerden cuando hace muchos años quemaban a los físicos por decir que la tierra era esférica, donde como siempre, la iglesia decía que eran unos blasfemos porque ellos afirmaban que era plana, bueno... esto es porque la tierra es localmente euclídea (una variedad) , es decir... es homeomorfa a la esfera de dimensión 2     $latex \mathbb{S}^2$ por lo que los religiosos por verla localmente euclídea pensaban que su forma era de $latex \mathbb{R}^2$ .
(ver la definición de variedad diferenciable y variedad en otro recurso en línea si así no te quedó claro antes de continuar).

Definición: Un mapeo suave $latex \gamma : [a,b] \rightarrow M$ de un intervalo a una subvariedad diferenciable $latex M \subset \mathbb{R}^n$ es una curva suave en $latex M \\$


Definición: Sea $latex M \subset \mathbb{R}^n$ una variedad diferenciable, y $latex p \in M$.
Un vector $latex v \\$ es un vector tangente a $latex M \\$ en $latex p$ si existe una curva suave $latex \gamma_{p}:[-\epsilon,\epsilon]\rightarrow M$ que pase por $latex p =\gamma_{p}(0)$  tal que $latex v=\gamma_{p}\prime (0)$, El espacio tangente $latex T_{p}M$ de $latex M \\$ en $latex p \\$ es el conjunto de todos los vectores tangentes a $latex M \\$ en $latex p \\$

Teorema:
Sea $latex M \\ $ una variedad en $latex \mathbb{R}^n$ de dimensión k, entonces tenemos que  $latex \forall p \in M$ existe un abierto $latex U \ni p$  tal que $latex M \\$ está definida en $latex U \\$ como la solución de un sistema de $latex (n-k) \\$ funciones reales diferenciables $latex \rho_{1}, ..., \rho_{n-k}$ definidos en $latex U \\$, es decir:

$latex (\rho_{1}=0)\cap ... \cap (\rho_{n-k}=0)=M\cap U$

y $latex \forall p \in M \cap U$, los vectores

$latex \nabla \rho_{1}(p),...,\nabla \rho_{n-k}(p)$

son linealmente independientes y:

$latex T_{p}M= generado\lbrace \nabla \rho_{1}(p),...,\nabla \rho_{n-k}(p) \rbrace ^{\perp}$

y $latex dim(T_{p}M)=k$

Es fácil ver que la definición con curva suaves y la del espacio ortogonal de los gradientes son equivalentes, aquí esbozo la demostración:


Sea $latex \gamma:[-\epsilon,\epsilon]\rightarrow M$ con funciones coordenadas $latex \gamma_{1}, ... \gamma_{n}$

Y tenemos que $latex M \\$ está definida por las $latex f_{i} \\$ :

$latex f_{i}(\gamma_{1}(t), ..., \gamma_{n}(t)) = 0$     $latex \forall t \in [-\epsilon, \epsilon]$    $latex 1 \leq i \leq n-k$

Esto sucede porque la imagen de $latex Im(\gamma) \subset M$, si diferenciamos (jacobiana) con respecto a $latex t \\$  tenemos que por la regla de la cadena:

$latex \frac{\partial{f_{i}}}{x_{1}}(x(0))x_{1}\prime (0)+...+\frac{\partial{f_{i}}}{x_{n}}(x(0))x_{n}\prime (0)=0$    $latex \Leftrightarrow \nabla f_{i}(x(0)) \cdot x\prime (0)=0 \Leftrightarrow$ $latex \nabla f_{i}(x(0) \perp x\prime (0)$
$latex \square \\$

Ahora vamos definir el concepto final de este post para terminar de ver de que trata la estructura del espacio tangente.


Definicion: Denotemos por $latex (f,U)$ a un abierto de $latex M \\$ tal que $latex p\in U$ y $latex f \\$ diferenciable en $latex U$, decimos que:

$latex (f,U) \sim (g,V)$

Si en el abierto $latex U \cap V$ tenemos que $latex f=g$ , esto claramente es una relación de equivalencia por lo que podemos definir el espacio vectorial:

$latex C_{p}^{\infty} =\lbrace (f,U) \rbrace / \sim $

El espacio tangente $latex T_{p}M$ consiste en todos los mapeos lineales:

  $latex d:C_{p}^{\infty} \rightarrow C_{p}^{\infty}$

Tal que:

$latex d(fg)=fd(g)+gd(f)$

Es decir que cumplen la regla de Leibniz (son derivaciones!)

Este espacio es muy importante ya que captura las propiedades de funciones cercanas a $latex p \\$


Eduardo Ruiz Duarte (beck)
rduarte@ciencias.unam.mx
@toorandom

k-formas diferenciales y derivada exterior (Parte 2/2, k-formas diferenciales y derivada exterior de éstas)

Como vimos, las 1-formas elementales son la proyección en una coordenada, ahora veamos a los operadores diferenciales como k-formas en $latex \mathbb{R}^n$ donde sus coordenadas son $latex x_{1},x_{2},...,x_{n}$:

El punto de estos posts es poder hacer la construcción de las k-formas diferenciales en la topología de Zariski para poder justificar el cálculo de singularidades en variedades sobre cualquier campo algebraicamente cerrado de caracteristica p o 0
Y al final de este artículo construiremos con las k-formas diferenciales el rotacional, la divergencia y gradiente (hablando en términos de campos vectoriales en $latex \mathbb{R}^n$)

Sea $latex \mu=\lbrace i_{1}, ..., i_{k}\rbrace$ una subsucesión de
$latex \Omega = \lbrace 1,2,...,n \rbrace$, tal que $latex 1 \leq i_{1} < ... < i_{k} \leq n$  y sea


$latex \displaystyle dx_{\mu}=d{x_{i_{1}}}\wedge ... \wedge d{x_{i_{k}}}$

Una k-forma diferencial $latex \omega$ es:

$latex \omega = \sum_{|\mu|=k}{f_{\mu}dx_{\mu}}$

Donde $latex f_{\mu}$ es una función diferenciable, y $latex \mu \subset \Omega$ está ordenado de manera creciente y $latex |\mu|=k$, por ejemplo una 1-forma en $latex \mathbb{R}^{2}$:
$latex (x+cos(y))dx+xydy$


Y una 2-forma en $latex \mathbb{R}^{3}$

$latex e^{x+y}dx\wedge dz + y^{3}dy \wedge dz$


Cada k-forma diferencial define para todo punto en $latex \mathbb{R}^{n}$ una k-forma diferente por ejemplo la 1-forma $latex (x+sen(y))dx + xydy$ es la 1-forma $latex 3dx$ en el punto $latex (3,0)$ y es $latex 5dx+2\pi dy$ en el punto $latex (4,\frac{\pi}{2})$



Pa definir la derivada exterior, primero necesitamos ver que es la derivada exterior de una 0-forma (función diferenciable, es decir que esté definida bajo un operador diferencial... o sea un operador que cumpla la regla de Leibnitz, esto puede ser la derivada normal como la conocemos también) y por inducción se definirá la derivada exterior para una k-forma en general

Dada una función diferenciable (0-forma) $latex f(x_{1},...,x_{n})$, su derivada exterior será denotada como $latex d f$  y es:

$latex df=\sum_{i=1}^{n}{\frac{\partial{f}}{\partial x_{i}}dx_{i}}$


Por ejemplo:
Si $latex f(x,y)=xy-y^{3}$ su derivada exterior $latex d f$ es:

$latex df=ydx+(x+3y^{2})dx$



Esto se parece al gradiente (PARECE)
Ahora definiremos lo que es la derivada exterior de una k-forma $latex \omega = \sum_{|\mu|=k}{f_{\mu}dx_{\mu}}$ con  $latex \mu=\lbrace i_{1}, ..., i_{k}\rbrace$ ordenada creciente:


$latex d \omega = \sum_{|\mu|=k}{df_{\mu}\wedge dx_{\mu}} $

Veamos un ejemplo con la derivada de una 1-forma fácil:

Sea $latex \omega = f_{1}dx_{1} + f_{2}dx_{2} + f_{3}dx_{3}$ una 1-forma de $latex \mathbb{R}^3$, entonces:

$latex d \omega = df_{1}dx_{1}+df_{2}dx_{2}+df_{3}dx_{3}=$
$latex \Bigg ( \frac{\partial{f_{1}}}{\partial{x_{1}}}dx_{1}+\frac{\partial{f_{1}}}{\partial{x_{2}}}dx_{2}+\frac{\partial{f_{1}}}{\partial{x_{3}}}dx_{3} \Bigg )\wedge dx_{1}+$
$latex \Bigg ( \frac{\partial{f_{2}}}{\partial{x_{1}}}dx_{1}+\frac{\partial{f_{2}}}{\partial{x_{2}}}dx_{2}+\frac{\partial{f_{2}}}{\partial{x_{3}}}dx_{3} \Bigg )\wedge dx_{2}+$
$latex \Bigg ( \frac{\partial{f_{3}}}{\partial{x_{1}}}dx_{1}+\frac{\partial{f_{3}}}{\partial{x_{2}}}dx_{2}+\frac{\partial{f_{3}}}{\partial{x_{3}}}dx_{3} \Bigg )\wedge dx_{3}=$
$latex \Bigg ( \frac{\partial{f_{3}}}{\partial{x_{1}}} - \frac{\partial{f_{1}}}{\partial{x_{3}}} \Bigg ) dx_{1} \wedge dx_{3} + \Bigg ( \frac{\partial{f_{2}}}{\partial{x_{1}}} - \frac{\partial{f_{1}}}{\partial{x_{2}}} \Bigg ) dx_{1} \wedge dx_{2} + \Bigg ( \frac{\partial{f_{3}}}{\partial{x_{2}}} - \frac{\partial{f_{2}}}{\partial{x_{3}}} \Bigg ) dx_{2} \wedge dx_{3} $

Ufff.. imaginen escribir eso en latex inline en blogspot... pero bueno

Eso también se parece al rotacional del campo vectorial $latex (f_1,f_2,f_3)$ (PARECE)

Cómo ya se habrán dado cuenta para toda k-forma diferencial $latex \omega$ se tiene que $latex d(d\omega)=0$, eso lo pueden demostrar fácilmente suponiendo la anticonmutatividad del operador cuña y que el orden de diferenciación no afecta a la función diferenciable, es decir:

$latex \frac{\partial{}}{\partial{x_{i}}} \frac{\partial{f}}{\partial{x_{j}}} = \frac{\partial{}}{\partial{x_{j}}} \frac{\partial{f}}{\partial{x_{i}}}$ y que $latex dx_{i}\wedge dx_{j}=-dx_{j}\wedge dx_{i}$

Ahora como ven, hice hincapié en la palabra "parece" al decir que habíamos encontrado el rotacional y el gradiente en términos de k-formas, veamos cómo son estas cosas en $latex \mathbb{R}^3$ con coordenadas $latex x,y,z$, vamos a definir una funciones que nos ayudarán a que no "parezcan" sino que "sean"


Sean:
$latex \omega_{0}=f(x,y,z)$
una 0-forma

$latex \omega_{1}=f_{1}(x,y,z)dx+f_{2}(x,y,z)dy+f_{3}(x,y,z)dz$
una 1-forma en general

$latex \omega_{2}=f_{1}(x,y,z)dx\wedge dy + f_{2}(x,y,z)dx\wedge dz \wedge f_{3}(x,y,z)dy\wedge dz$
una 2-forma elemental general

Y como la única 3-forma elemental en $latex \mathbb{R}^{3}$ es $latex dx\wedge dy\wedge dz$ tenemos que una 3-forma elemental general sería de la forma:

$latex \omega_{3}=f(x,y,z)dx\wedge dy \wedge dz$

Donde $latex f_{i},f\in \mathfrak{F}(\mathbb{R}^{3})$ (funciones en $latex \mathbb{R}^{3}$)

Definimos las siguiente funciones: entre formas y funciones de $latex \mathbb{R}^{3}$ denotadas por $latex \mathfrak{F}(\mathbb{R}^{3})$ y formas con campos vectoriales de $latex \mathbb{R}^{3}$ denotadas por $latex \Delta(\mathbb{R}^{3})$

$latex \displaystyle \theta_{0}: {\bigwedge}^{0}{\mathbb{R}^{3}} \rightarrow \mathfrak{F}(\mathbb{R}^{3})$

    $latex \omega_{0} \mapsto f$

$latex \displaystyle \theta_{1}: {\bigwedge}^{1}{\mathbb{R}^{3}} \rightarrow \Delta(\mathbb{R}^{3})$

    $latex \omega_{1} \mapsto (f_{1},f_{2},f_{3})$

$latex \displaystyle \theta_{2}: {\bigwedge}^{2}{\mathbb{R}^{3}} \rightarrow \Delta(\mathbb{R}^{3})$

    $latex \omega_{2} \mapsto (f_{3},-f_{2},_f_{1})$

$latex \displaystyle \theta_{3}: {\bigwedge}^{3}{\mathbb{R}^{3}} \rightarrow \mathfrak{F}(\mathbb{R}^{3})$

    $latex \omega_{3} \mapsto f(x,y,z)$

Esto ¿para qué?, como vemos $latex \theta_{0}$ es la identidad y estas definiciones tienen una manera natural de ser, ya que si hacen la talachita pueden demostrar el siguiente teorema:

Teorema: En $latex \mathbb{R}^{3}$, si $latex \omega_{s}$ es una s-forma entonces

$latex \theta_{1}(d\omega_{0})=\nabla \theta_{0}(\omega_{0})=\vec{\nabla f}=grad(\theta_{0}(\omega_{0}))$
$latex \theta_{2}(d\omega_{1})=\nabla \times \theta_{1}(\omega_{1})=rot({\theta_{1}(\omega_{1})})$
$latex \theta_{3}(d\omega_{2})=\nabla \cdot \theta_{2}(\omega_{2})=div({\theta_{2}(\omega_{2})})$
$latex \square$

Cada uno de los cálculos se puede hacer explícitamente y no hay mucho que pensar en la demostración más que talacha dura, y con esto tenemos ya en términos de formas diferenciales lo que es el gradiente, rotacional y divergencia

El punto de estos posts es poder llegar a definir esto en términos de geometría algebraica en variedades usando la topología de Zariski

Eduardo Ruiz Duarte (beck)
rduarte@ciencias.unam.mx
@toorandom

k-formas diferenciales y derivada exterior (Parte 1/2, k-formas $latex \wedge$)

Estos conceptos son de suma importancia en varias areas de matemáticas, no sólo en geometría diferencial, también en geometría algebraica por ejemplo al definir espacios tangentes con la topología de Zariski, pero también he visto que hay ciertas confusiones, por lo que trataré de dejar el concepto claro con lo que sé y mis notas del curso de geometría diferencial que tomé con el Dr. Gregor Weingart.
Para esto primero veremos lo que son las k-formas y el producto cuña en esta primera parte. 

Estoy suponiendo que el lector tiene conocimiento de lo que significa el determinante en términos de volumen, a grandes rasgos si tú tienes vectores en un espacio de Banach donde sí se vale el teorema de Ptolomeo (La relación entre los lados de un paralelogramo y sus diagonales), estos espacios de Banach son espacios de Hilbert y pueden dar luz a un único producto interno, y con este al determinante, ejemplos de estos espacios son los famosos $latex \mathbb{R}^n$ y $latex \mathbb{C}^m$, así que regresando al determinante formando la matriz $latex A=(v_1,...,v_k)$
y consideras $latex A^{T}$ entonces el volumen del paralelepípedo generado por los vectores $latex \lbrace v_1, ..., v_k \rbrace$ es $latex \sqrt{det(A^{T}A)}$, si te cuesta trabajo visualizarlo, imagina sólamente un vector $latex A=v \in \mathbb{R}^{n}$ , tenemos que $latex \sqrt{det(A^{T}A)}=\sqrt{det(v\cdot v)}=\sqrt{det({a_1}^{2}+...+{a_n}^{2})}=\sqrt{{a_1}^{2}+...+{a_n}^{2}}=||{v}||$
el cual pues es el "volumen" (longitud) del vector.

Trataremos primero de entender 2-formas elementales en $latex \mathbb{R}^3$, y llamaremos $latex x_1,x_2,x_3$ los ejes coordenados de $latex \mathbb{R}^3$. Ahí tendremos tres 2-formas elementales que serán denotadas por $latex dx_1 \wedge dx_{2} , dx_{1} \wedge dx_{3}, dx_{2} \wedge dx_{3}$

En palabras burdas, $latex dx_{i} \wedge dx_{j}$ es un operador que es el area (con signo) de la proyección en el plano $latex x_{i}x_{j}$ de un paralelepípedo en  $latex \mathbb{R}^3$.

Como ejemplo, a mi me lo explicaron siempre suponiendo que ya lo conocía... a veces necesito ejemplos para poder entender lo que me están diciendo o demostrando.

Considera los vectores $latex {v_{1}}^{T}=(1,2,3)$ y $latex {v_{2}}^{T}=(3,2,1)$ , si los dibujan verán que forman un paralelepitedo $latex P$ en $latex \mathbb{R}^3$, considera la proyección:

$latex \rho : \mathbb{R}^3 \rightarrow \mathbb{R}^2$
$latex (x_1,x_2,x_3) \mapsto (x_1,x_2)$

Es decir de $latex \mathbb{R}^3$ al plano $latex x_{1} x_{2}$

Definimos $latex dx_{1} \wedge dx_{2}$ actuando en el paralelepípedo $latex P$ como el area de
$latex \rho(P)$ es decir:

$latex dx_{1}\wedge dx_{2}(P)=A(\rho (P) )$

Entonces tenemos que $latex \rho(P)$ es el paralelogramo en este ejemplo formado por $latex \rho(v_{1})$ y $latex \rho(v_{2})$ es decir por los vectores $latex (1,2)$ y $latex (3,2)$

Esto nos dice que:

$latex dx_{1} \wedge dx_{2}(P)=det(\rho(v_{1}),\rho(v_{2}))= det\begin{pmatrix} 1& 3\\2&2 \end{pmatrix}=-4$

En general en $latex \mathbb{R}^{3}$ , dados dos vectores columna que forman un paralelogramo $latex v_{1}^{T}$ y $latex v_{2}^{T}$ para la matriz $latex A=(v_{1}^T,v_{2}^T)=\begin{pmatrix} a_{11}&a_{12}\\a_{21}&a_{22}\\a_{31}&a_{32} \end{pmatrix}$
Tenemos que el area del paralelogramo en la proyección en el plano $latex x_{1}x_{2}$ es:

$latex dx_{1}\wedge dx_{2}(A)=det \begin{pmatrix} a_{11}& a_{12}\\a_{21}&a_{22} \end{pmatrix}$

De manera similar para los planos $latex x_{i}x_{j}$

Ahora, cuando vemos una integral $latex \int{f(x)}dx$ el significado de dx lo puedes deducir como una 1-forma que es la longitud en el eje x, este operador es el "volumen" en una dimensión como lo mencioné al inicio de este post, el "volumen" aquí es la longitud, por lo que:

Si $latex v=(a_{i},a_{j},a_{k})$ entonces $latex dx_{s}(v^{T})=a_{s}$ el cual es la proyección $latex \rho_{s}$ en la s-ésima coordenada.

Ahora cómo generalizamos esto a k-formas?, es decir, este operador $latex \wedge$ queremos que nos calcule el volumen de paralelepípedos k-dimensionales en un espacio de Hilbert n-dimensional, en este caso usamos $latex \mathbb{R}^{n}$

Para la generalización en $latex \mathbb{R}^{n}$ , tenemos que si sus coordenadas son $latex x_1,x_2,...,x_n$ Si tenemos una subsucesión $latex \Omega=(i_1,i_2,..,i_k)$ de tamaño $latex k$ de $latex (1,2,...,n)$ donde $latex 1\leq i_{1}< ...< i_{k} \leq 1$
$latex A=\begin{pmatrix} a_{11}&a_{12}&\cdots &a_{1k}\\ \vdots&\vdots&\vdots &\vdots\\ a_{n1}&\cdots &\cdots& a_{nk} \end{pmatrix}=\begin{pmatrix}A_{1}\\ \vdots \\ A_{k}\end{pmatrix}$ Es una matriz de $latex n\times k$ donde sus columnas generan el paralelepípedo k-dimensional en $latex \mathbb{R}^{n}$, denotamos sus renglones por $latex A_{i}$
Lo que queremos es un operador que actúe en la matriz $latex A$ para darnos el (hiper)volumen del paralelepipedo proyectado en el (hiper)espacio $latex {x_{i}}_{1} {x_{i}}_{2}...{x_{i}}_{k}$ por lo que la k-forma es el siguiente operador:

$latex \displaystyle dx_{\Omega}=d{x_{i}}_{1} \wedge d{x_{i}}_{2}\wedge ...\wedge d{x_{i}}_{k}$

Donde

$latex \displaystyle {dx}_{\Omega}(A)=d{x_{i}}_{1} \wedge d{x_{i}}_{2}\wedge ...\wedge d{x_{i}}_{k}(A)=det \begin{pmatrix}A_{i_{1}}\\ \vdots \\ A_{i_{k}}\end{pmatrix} $

Ya con esto es suficiente para que puedas comenzar a jugar, es decir... este producto es conmutativo ?
La respuesta es NO, depende, pero no es tan grave, es anticonmutativo en el caso de 1-formas esto es porque para un paralelepípedo P
$latex dx_{i} \wedge dx_{j}(P)=det(\rho(v_{i}),\rho(v_{j}))=-det(\rho(v_{j}),\rho(v_{i}))=-dx_{j} \wedge dx_{i}(P)$
al final es una propiedad elemental de matrices, al cambiar columnas o renglones se alterna el signo, por lo que tenemos que este es un operador alternante
, ahora, aquí usamos el determinante, pero todos los operadores que tengan las características del determinante serán k-formas

De hecho decimos que una k-forma real $latex \omega$ sobre $latex \mathbb{R}$ es es una función:

$latex \omega :M_{nk}(\mathbb{R})\rightarrow \mathbb{R}$

Que satisface multilinearidad, lo cual se expresa usando como argumento para $latex \omega$ la matriz de $latex n\times k$ separada por columnas $latex \Lambda=(A_{i},...,\lambda B + \mu C,...,A_{k})$:

$latex \omega(\Lambda)=\omega(A_{1},...,\lambda B+ \mu C, ..., A_{k})=\lambda \omega(A_{1},...,B,...,A_{k})+\mu \omega(A_{1},...,C,...,A_{k})$

Es decir las propiedades del determinante, pero estas funciones alternantes son en general, es por eso que a las k-formas primeras les llamamos "elementales" , pero estas son las generales.

Ya con esto el teorema principal que no demostraré, pero ya se imaginarán el por qué de su veracidad es el siguiente:

Teorema: Las k-formas del espacio vectorial $latex \mathbb{R}^{n}$ forman un espacio vectorial de dimensión $latex \begin{pmatrix}n\\ k\end{pmatrix}$ donde las k-formas elementales forman una base para éste, este espacio vectorial se denota como $latex \displaystyle {\bigwedge}^{k}(\mathbb{R}^{n})$
$latex \square$

Ahora, si $latex \tau,\sigma$ son l-forma y k-forma respectivamente tenemos que
$latex \tau \wedge \sigma = (-1)^{lk}\sigma \wedge \tau=0 \Leftrightarrow l,k$ son impares

(en el caso de 1-formas por eso se alterna el signo) esto es fácil demostrarlo con lo que hemos visto, sólo tienes que desarrollar el producto cuña bien con una k-forma y una l-forma en general

Ahí se ve lo que pasa con la alternancia. Para esto puedes demostrar que el producto cuña ($latex \wedge$) de dos 1-formas te da 2-formas, y con las propiedades de alternancia y multilinearidad podemos definir lo que es una k-forma diferenciable y la derivada exterior, pero esto lo veremos en la parte 2 de este post
Espero les haya servido de algo
Eduardo Ruiz Duarte(beck)
rduarte@ciencias.unam.mx

Mi opinion sobre la actual situación con la CNTE y la reacción social

No creo que todas las opiniones sean al tanteo o por vanidosos o idiotas o desinformados... es más creo en la paradoja de que todos estamos mal y todos estamos bien a la vez. Esta situación tiene miles de matices, ya que ambas partes defienden algo políticamente correcto... y por otro lado en el PRI son una bola de corruptos que es imposible creer que lo hacen por tu bien, y esto que hacen es a simple vista sólo para recuperar el control del magisterio ya que la educación no es prioridad para EPN. Sí... hasta aquí si eres PRIista dejarás de leerme porque has de creer que soy un AMLOver o no sé...pero no la verdad.

La gente critica mucho al gobierno o a los maestros... ¿tu de qué lado estás?

Esta situación por más que leas y leas de izquierda y derecha no llegarás a nada NUNCA y sólo emitirás juicios de valor o borreguearás o simplemente sentirás que es "correcto apoyar a los jodidos" (lástima disfrazada), explico el por qué de mi opinión:

Los maestros tienen miedo de afectar los estímulos de su carrera magisterial debido a una incongruencia por parte de la SEP en las razones de evaluación, entre otras cosas las cuales tienen razón.

Por otro lado el neoCNTE heredó la dinámica de EEG y se compran plazas vitalicias por 30 mil pesos sin criterios de evaluación por parte de la SEP permitiendo que cualquier estúpido "eduque" porque el sindicato así ha peleado por su autonomía profesional...

"sí... que los maestros se manifiesten... cantemos sus consignas... a huevo sí sí!!! pinche gobierno de mierda priista los odio por afectar la libertad de expresión del CNTE... y estoy a favor de los pobres"

blah blah eso diría cualquier pseudo izquierdista promedio hipster de toda la vida clasemediero... pero quiero ver que a su banda le toque ser educada por los beneficiados del nepotismo o corrupción de las plazas... Pero un segundo... ahh no... sólo le tocarán a los 40 millones de personas de clase baja (jodidísimas) que te importan un carajo y se están pudriendo en pobreza y no a ti, qué fácil es decir eso no?, hay muchísimos niños afectados hoy en día que no están aprendiendo a leer, escribir, sumar, et cétera... ya sea por pseudo maestros o maestros porque no dudo que haya buenos maestros.

Por otro lado defendiendo a los maestros desde otra arista... en el gobierno sabemos que desde hace mucho no ha hecho algo para el bien de todos..., de hecho esto como lo dije anteriormente es para tener el control, las escuelas están hechas una mierda, pueblos olvidados como Unión de Guadalupe que me tocó conocer en la huasteca potosina, entre otros y el gobierno se ha dedicado a NO educar para comprar votos... y los indígenas están olvidados as always... México es un país en el que sus dirigentes se dedican a satisfacer intereses particulares a través de una cadena de favores, olvidando la esencia... la cual es el bienestar nacional.

Todo esto tiene que ver con la falta de interés por el país, y los maestros aquí son víctimas por el hecho de no
ser tomados en cuenta como pilar para garantizar la capacidad de criterio de los futuros ciudadanos, tal vez el plan es ese... dejar a todos en la ruina intelectual para poder seguir haciendo lo que se les pegue la gana.

Esto creo va ligado también con la sed de poder y la educación por generaciones de un pueblo reprimido por España, sintiéndose siempre "dominado" por lo que al tener poder, se desencadena toda la porquería que implica la avaricia.

Por lo que digo... cualquier opinión sobre la CNTE y el gobierno, positiva o negativa para quién sea funciona debido a que cualquiera prácticamente es correcta ya que la paradoja lógica es que ambos están mal y ambos están bien desde cualquiera de las variables.

Creo que cualquiera defendiendo una postura específica será un ULTRA y jamás alguno podrá concientizar al otro de su punto, debido a que en ambos lados hay obscuridad.

Si eres el que dice que la CNTE está mal por X o Y razón entonces eres un neoliberal conservador priista anti proletariado enemigo de la raza

Creo que la solución no está en hacer paros académicos, esto de sólamente solidarizarse con la CNTE me parece inútil.

En el caso contrario eres el anarquista, desinformado, el antiproyecto de nación, el AMLOver, el apestoso, el comunista o el que no ha forjado su criterio leyendo e informándose desde la derecha Y la izquierda

¡Qué paradójico! ¿no? , yo también sería un  ultra por discriminar a aquellos que tienen una postura definida en algo tan ambiguo.

Reunámonos todos los que podamos para proponer una nueva reforma educativa, hagamos foros de discusión, creo que esto es mejor y ayudará a que la gente tome conciencia con argumentos realmente sólidos de gente pensante, la situación de paro académico se me hace la posición más comodina, si vamos a hacer algo, que sirva y como lo dije, repito... propongamos una nueva reforma educativa, porque digan lo que digan, sí es necesaria, tal vez no como está planteada, pero la CNTE está fuera de control y con dádivas excesivas gracias a su autonomía


saludos

Sobre las malas opiniones y el debate serio

Odio que opinen sin leer o documentarse y causen polémica barata haciendo juicios de percepción como si fueran la realidad y no de hechos verdaderos y que te digan "tengo derecho a opinar", NO , si no sabes no puedes opinar, es una ley de la vida, Un punto de vista indocumentado y falso puede conducir a polémica absurda con los debatientes y hacerlos dudar de lo que es correcto y de lo que no es en ese contexto; sólo por el hecho de que te respetan y piensan que lo que dices es producto de tu inteligencia y ellos no saben que sólo lo escupiste por lucirte o por no quedar atrás o yo qué sé.

Aquí unos tipos de debate y como sobrellevarlos para una mejor opinión

1. Cuando lo que se está debatiendo son juicios de valor o de percepción es absolutamente válido meter lo que dices basado en tu manera de sentir sin utilizar datos previos

2. Para debatir de política hay que conocer lo que respetas y lo que no, ahí el punto de vista puede llegar a ser sumamente objetivo, tienes que estar documentado de varias caras del tema, eso indicaría que has forjado bien tu criterio como para poder opinar.

3. Cuando debates de ciencia (método científico) lo único que puedes afirmar son resultados VERDADEROS o puedes SUPONER resultados BASADOS en situaciones similares o que impliquen transitivamente el hecho a debatir, el afirmar algo que "ADIVINAS" está completamente fuera del método científico y más aún si tú afirmas "Yo soy el físico aquí, CRÉEME". NO, eso es una falacia, no porque lo seas significa que conoces el resultado, tienes que mostrarlo.

4. Cuando debates matemáticas lo único que puedes afirmar es lo demostrable o en el caso de metamatemática, lo que tus axiomas te permitan poder demostrar más bien, en matemáticas no hay experimentación ni observación, ahí las cosas son claras.

5. Cuando opinas sobre personas o grupos de personas es donde más cuidado debes tener ya sea que digas algo positivo o negativo, generalmente cuando se habla positivamente de alguien es por cordialidad (a veces no) y eso pierde la objetividad de las cosas y negativamente tienes que tomar en cuenta que puedes manchar la imagen de alguien que le podría afectar directamente si tu opinión está basada en hechos personales, aquí es donde más hay que documentarse de lo que se dice ya que un mal comentario también puede afectarte a ti como crítico y confundir tu perspectiva por un simple "chisme"

No es que "no tengas derecho" per sé a opinar.

todos tenemos el derecho a decir tonterías

Pero si quieres que este país avance más rápido, se necesitan opiniones objetivas y bien documentadas con el fin de no atrasar a los demás.

No te haces el inteligente cuando opinas sin saber, todo lo contrario.

De hecho, te ves más inteligente cuando aceptas tu ignorancia.

Esto que digo, es algo que sentí como de "moraleja" del libro de Noam Chomsky "Piratas y Emperadores"

Muchas guerras, conflictos, etcétera se podrían haber evitado con el mejor uso de la lengua: gramática, sintaxis, semántica y obviamente lo que menciono... una buena opinion sobre las cosas.

Se los recomiendo


Saludos


Eduardo Ruíz Duarte (beck)