Teorema de Riemann-Roch y divisores en criptografía, (Parte 3: valuaciones, espacios de Riemann, su dimensión, género y curvas elípticas sin Bézout)

Vimos en la parte 1 el anillo de funciones regulares en una variedad y su localización en un punto, así como las funciones en un abierto de la variedad bajo la topología de Zariski, en la parte 1 de estos posts.

Ahora lo que queremos es justificar la estructura de grupo de una curva elíptica y si nos da tiempo de una hiperelíptica de género 2, pero para eso debemos introducir el concepto de divisores sobre la variedad y "género" el cual estará estrechamente relacionado con la dimensión de un espacio vectorial de funciones generado con un divisor.


Valuaciones


Vamos a suponer que $latex \mathbb{K}$ es un campo arbitrario el cual será un campo de constantes de algo más grande... el campo de funciones.

Definición 1: Una extensión $latex \mathbb{F}$ de $latex \mathbb{K}$ es un campo de funciones algebraico en una variable sobre $latex \mathbb{K}$ si existe un $latex z\in \mathbb{F}$  trascendente sobre $latex \mathbb{K}$ de tal manera que $latex [\mathbb{F}:\mathbb{K}(z)]$ es finita.


Los objetos centrales en esto serán los lugares, denotados por $latex P$ que de manera resumida serán los ideales máximos de todos los anillos de valuación que existan en $latex \mathbb{F}$ recuerden que los anillos de valuación son locales por lo que sólo tienen un ideal máximo, este anillo como en la parte uno lo denotaremos por $latex O_p$ y su ideal máximo como $latex M_p$


Recuerden como eran las funciones regulares de una variedad $latex V$ en un punto de la parte 1 de este blog la cual habíamos denotado como $latex O_p(V)=\lbrace f/g \in \mathbb{K}(V) : g(p)\neq 0 \rbrace$

Nota 1:
Aquí tenemos que $latex \mathbb{F}$ tiene un elemento trascendente y es campo por lo que podemos imaginarlo como que es on cociente de funciones polinomiales en una variable, pero podría ser que $latex \mathbb{K}$ sea ya un campo de funciones y $latex z\in \mathbb{F}$ otro elemento trascendente, haciendo que el campo de constantes no sea tan trivial.

Definición 2: Una valuación discreta normalizada de un campo de funciones algebraico $latex \mathbb{F}$ sobre $latex \mathbb{K}$ es un mapeo suprayectivo:


$latex \nu:\mathbb{F}\rightarrow \mathbb{Z}\cup \lbrace \infty \rbrace$

que satisface:

1. $latex \nu(f)=\infty \Leftrightarrow f=0$
2. $latex \nu(fg)=\nu(f)+\nu(g)$      $latex \forall f,g\in\mathbb{F}$
3. $latex \nu(f+g) \geq min(\nu(f),\nu(g))\Rightarrow\nu(f+g)=min(\nu(f),\nu(g))$     $latex \forall f,g\in \mathbb{F}$
4. $latex \nu(a)=0$       $latex \forall a\in \mathbb{K}^{*}$

Estos mapeos están en correspondencia biunívoca con los lugares de $latex \mathbb{F}$ por lo que si $latex P$ es un lugar de $latex \mathbb{F}$ definiremos como $latex \nu_P$ a su valuación correspondiente y denotaremos por $latex \mathbb{P}_\mathbb{F}$ a el conjunto de todos los lugares de $latex \mathbb{F}$ 

Nota 2: Recordemos que cuando vimos en la parte 1 el anillo de funciones regulares en una variedad, tenemos que los puntos están en correspondencia con los ideales máximos, aquí estámos usando por eso los lugares que son los ideales máximos pero lo estamos generalizando un poquito más con estas estructuras, que en vez de considerar los puntos , consideramos los ideales máximos de la localización.

Ahora vamos a definir los anillos locales en términos de valuaciones y lo ilustraremos con un ejemplo sencillo, estos anillos serán llamados anillos de valuación discreta de $latex \mathbb{F}$ correspondientes al lugar $latex P\in \mathbb{P}_\mathbb{F}$

$latex O_P=\lbrace f\in \mathbb{F} : \nu_P(f) \geq 0\rbrace$

Es fácil demostrar que es un anillo local, basta considerar quiénes son los elementos invertibles para saber que su ideal máximo (que obviamente no tiene elementos invertibles) es:

$latex M_P = \lbrace f\in O_P : \nu_P(f)>0 \rbrace$

Como $latex M_P$ es máximo definiremos el campo residual 

$latex \hat{\mathbb{F}}_P:=O_P/M_P$ 

y definiremos el grado de $latex P$ como el grado de la extensión $latex grad(P):= [\hat{\mathbb{F}}_P:\mathbb{K}]$ , cuando $latex grad(P)=1$ diremos que $latex P$ es racional

Bueno, yo recuerdo que cuando leí esto por primera vez se me hacía muy mágico el mapeo $latex \nu_P$ 

por lo que creo que es conveniente ilustrarlo con un ejemplo.

Ejemplo:

Sea $latex \mathbb{F}=\mathbb{K}(x)$ con $latex x$ trascendente sobre $latex \mathbb{K}$ es decir estamos considerando todos los cocientes de polinomios en una variable sobre el campo $latex \mathbb{K}$ aquí tenemos que los mónicos irreducibles $latex P(x)\in \mathbb{K}[x]$  nos inducen una valuación discreta única $latex \nu_P$

$latex \nu_P(f(x)) = r$ si $latex f(x)\in \mathbb{K}[x]-\lbrace 0 \rbrace$ y $latex P(x)^r \mid f(x)$

$latex O_P = \Bigg \lbrace \frac{f(x)}{g(x)} \in \mathbb{F} : P(x)\nmid g(x) \Bigg \rbrace$

Es clara esta definición ya que si $latex P(x)\mid g(x)$ es decir no se cancela en $latex f(x)$ la valuación sería negativa y tenemos que el anillo está formado por los elementos que tienen valuación mayor o igual que cero

Ahora, su ideal máximo ¿quién es?, tenemos que no tiene que tener elementos invertibles en $latex O_P$ y que su valuación sea estrictamente mayor que 0, eso significa que $latex P(x) \mid f(x)$ y como es subconjunto de $latex O_P$ también tiene que suceder que $latex P(x) \nmid g(x)$  por lo que en símbolos.

$latex M_P=\Bigg \lbrace \frac{f(x)}{g(x)} \in \mathbb{F} : P(x)\mid f(x), P(x)\nmid g(x) \Bigg \rbrace$

Entonces a qué huelen los elementos invertibles de $latex O_P$ ?  pues son todos los que NO tienen a $latex P(x)$ involucrado en el cociente $latex \frac{f(x)}{g(x)}$ es decir , los que tienen su valoración exactamente 0.

Entonces en este ejemplo cuando $latex P$ es linealtenemos que 

$latex \mathbb{F}/(P(x)) \cong \mathbb{K}$ 

Es decir, los lugares $latex P$ RACIONALES son aquellos generados con polinomios mónicos lineales.

Aquí en este ejemplo y en todos los interesantes, es decir cuando consideremos curvas elípticas o hiperelípticas hay otro  anillo de valuación que no está asociado a un polinomio pero pueden demostrar que es anillo y que tiene un sólo ideal máximo

$latex O_\infty = \Bigg \lbrace \frac{f(x)}{g(x)} \in \mathbb{F}, g(x)\neq 0, grad(f(x)) \leq grad(g(x)) \Bigg \rbrace $

y su ideal máximo

$latex M_\infty =\Bigg \lbrace \frac{f(x)}{g(x)} \in \mathbb{F}, g(x)\neq 0, grad(f(x)) < grad(g(x)) \Bigg \rbrace $

Es fácil ver esto , y que los invertibles tienen el mismo grado tanto en el numerador como denonimador.

Esto le llamaremos el lugar infinito de $latex \mathbb{F}$ y como ejercicio podrían demostrar que $latex O_\infty/M_\infty \cong \mathbb{K}$  por lo que otra vez tenemos un lugar RACIONAL es decir, el lugar infinito es racional, si el lugar tiene relacionado un polinomio diremos que es finito.

Observación:

Si $latex \mathbb{K}=\mathbb{F}_q$ es finito entonces hay $latex q+1$ lugares racionales, el +1 es por el lugar infinito

Divisores

Los divisores son esencialmente sumas formales de lugares junto con un coeficiente, esto será intuitivamente una expresión que nos ayudará a juntar ciertas características de elementos del campo de funciones

Definición 3: Un divisor $latex D$ de un campo de funciones algebraico $latex \mathbb{F}$ es una suma formal:

$latex D=\sum_{P\in \mathbb{P}_\mathbb{F}}m_P P$

Donde un número finito de $latex m_P$ es distinto de cero, este conjunto de divisores los denotamos por $latex Div(F)$

El soporte de un divisor es:

$latex sop(D):= \lbrace P\in \mathbb{P}_\mathbb{F} : m_P \neq 0\rbrace$

El grado de un divisor es:

$latex \partial(D):=\sum_{P \in sop(D)} (m_P)grad(P)$

Se dice que un divisor $latex D$ es positivo/efectivo si todos sus $latex m_P$ son mayores o iguales que 0, y escribimos $latex \nu_P(D) \geq 0$ .

Si dos divisores $latex D_1,D_2 \in Div(\mathbb{F})$ los comparamos como $latex D_1 \leq D_2$ si $latex \nu_P(D_1) \leq \nu_P(D_2)$ para todo $latex P \in \mathbb{P}_\mathbb{F}$, es decir que todos los coeficientes de los sumandos de los divisores son menores o iguales.  

Es claro que $latex Div(\mathbb{F})$ forma un grupo abeliano con suma definida componente a componente y es un grupo libre, y que un subgrupo de éste son los divisores de grado 0, que lo denotaremos por $latex Div^0(\mathbb{F})$

Definición 4: Decimos que si $latex \nu_P(f)$ > $latex 0$  entonces $latex P$ es un cero de multiplicidad  $latex \nu_P(f)$ y si $latex \nu_P(f)$ < $latex 0$ decimos que es un polo

Es claro que las constantes no tienen ceros ni polos, pero los demas elementos $latex f\in \mathbb{F}$

tienen al menos un cero y un polo.

Definición 5: Sea $latex f\in \mathbb{F}^{*}$ y $latex Z(f),N(f)$ los ceros y los polos de $latex f$ respectivamente, entonces definimos:

divisor de ceros de $latex f$:

$latex (f)_0 = \sum_{P\in Z(f)}\nu_P(f)P$

divisor de polos de $latex f$:

$latex (f)_\infty = \sum_{P\in N(f)}-\nu_P(f)P$

divisor principal de $latex f$:

$latex div(f):=(f)_0 - (f)_\infty$

Aquí sucede algo que habría que demostrar y no es tan directo pero si es lógico.

Que todos los divisores principales tienen grado 0, es decir, $latex \partial(div(f))=0$ para todo $latex f\in \mathbb{F}^{*}$, o sea existe el mismo número de ceros y de polos  en los elementos de $latex \mathbb{F}$, esto lo pueden ver en el libro de Algebraic function fields and codes  de Henning Stichtenoth.

Definición 5: El espacio de Riemann-Roch para un divisor $latex D$ de $latex \mathbb{F}$ está definido como:

$latex \mathfrak{L}(D):= \lbrace f\in \mathbb{F}^{*} : div(f)+D \geq 0 \rbrace \cup \lbrace 0 \rbrace $

Este espacio es un espacio vectorial sobre $latex \mathbb{K}$ y su dimensión será denotada por $latex l(D)$


Hay cosas que podrían demostrarse por ejercicio que son muy directas como que $latex l(0)=1$ o que $latex l(D)=0$ si $latex \partial(D)$ < $latex 0$


Teorema (Riemann-Roch): Sea $latex \mathbb{F}$ un campo de funciones algebraico de género $latex g$ , entonces para cada divisor $latex D$ de $latex \mathbb{F}$ tenemos que:

$latex l(D)\geq \partial(D)+1-g$

donde la igualdad se da si $latex \partial(D)\geq 2g-1$


Este teorema es muy potente y sirve de clasificación para campos de funciones con respecto al género

Definición 6:
El género $latex g$ de un campo de funciones $latex \mathbb{F}$ se define como:

$latex g:= g(\mathbb{F}):=max_D(\partial(D)-l(D)+1)$

O sea el máximo de todos los divisores de $latex \mathbb{F}$, tenemos que el género del ejemplo $latex \mathbb{K}(x)$ es 0 y decimos que el campo de funciones $latex \mathbb{F}$ es elíptico si su género es 1

Definición 7:
Sea $latex P\in \mathbb{P}_\mathbb{F}$ , $latex \forall$ $latex n \geq 1$ es número de polo para $latex P$ si existe un elemento $latex f\in \mathbb{F}^{*}$ tal que $latex (f)_\infty = nP$, si no existe esto decimos que $latex n$ es número de salto para $latex P$

Corolario (Saltos de Weierstrass): 
Sea $latex \mathbb{F}$ de género $latex g\geq 1$ y sea $latex P$ un lugar racional de $latex \mathbb{F}$, entonces existen exactamente $latex g$ número de salto $latex i_j$ que satisfacen:

$latex 1=i_1$ < ... < $latex i_g \leq 2g-1$


Esto se sigue inmediatamente de que:

• $latex \forall i\geq 1$ tenemos que $latex \mathfrak{L}((i-1)P)\subseteq \mathfrak{L}(iP)$ y $latex \mathfrak{L}((i-1)P)=\mathfrak{L}(iP) \Leftrightarrow i$ es número de salto
• $latex l(iP)\leq l((i-1)P)+1$
• $latex l(0P)=1$ y $latex l((2g-1)P)=g$

Criptografía

Ya habíamos mencionado que todos los divisores de funciones tienen grado 0 es decir tienen el mismo número de ceros y de polos. por lo que estos serían un subgrupo de $latex Div^{0}(\mathbb{F})$

entonces el subgrupo de divisores principales lo denotamos como:

$latex Prin(\mathbb{F}):= \lbrace div(f) : f\in \mathbb{F}^{*}\rbrace \subset Div^{0}(\mathbb{F})$

Como estos grupos son libres, abelianos, podemos hablar de su cociente, por lo que el grupo que necesitamos para criptografía y el que se usa actualmente es el grupo de Picard de orden 0 el cual es isomorfo a:

$latex Pic^{0}(\mathbb{F}):= Div^0(\mathbb{F})/Prin(\mathbb{F})$


Si el género del campo de funciones $latex \mathbb{F}$ es 1 este grupo es isomorfo al grupo usual que conocemos de las curvas elípticas  y si es 2 se dice que es hiperelíptico.

De hecho, para culminar este post, vemos que no necesitamos el teorema de bézout para demostrar que una recta intersecta en 3 puntos a una curva proyectiva ya que:


Ya conocemos estas propiedades de los divisores de funciones por el hecho de que sabemos que tienen el mismo número de ceros que de polos por lo que:

Tenemos que si $latex f,g \in \mathbb{F}=\overline{\mathbb{K}}(C)$ es el campo de funciones de una curva elíptica (i.e. cúbica)

$latex div(f/g)=div(f)-div(g)$
$latex div(fg)=div(f)+div(g)$
$latex div(f^n)=n\cdot div(f)$


Nota sobre funciones en la curva:  Es importante considerar que para entender un objeto algebraico, hay que entender las funciones en éste, y si son proyectivos, cosas interesantes pasan, por ejemplo si tenemos la curva elíptica $latex C(x,y)=y^2 - x^3 + x$

Considera la función racional $latex q(x,y)= x/y \in \mathbb{F}=\hat{\mathbb{K}}(C)$ , podemos ver que $latex q(1,0)=\infty$ pero $latex q(0,0)=??$ , pero si usamos que esta función pertenece a la curva elíptica $latex C$ por lo que bajo la relación algebraica $latex y^2 = x^3 - x$ tenemos que $latex x/y = y/(x^2+1)$ por lo que en la curva, es decir en su campo de funciones $latex q(0,0)=0$.

Criptografía con campos de funciones elípticos vía teorema de Riemann-Roch.

Si consideramos la curva proyectiva elíptica $latex C$ homogeneizada con la variable $latex z$
aquí los ideales máximos son los puntos de la curva, y los anillos locales son las funciones racionales definidas en cada punto.

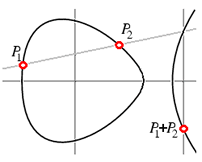
Si tomamos la linea $latex l_PQ$ que pasa por los puntos $latex P,Q \in \mathbb{P}_\mathbb{F}$

tal que la linea tiene pendiente finita, como demostramos en la parte 2, esta linea choca con otro punto al infinito que es el que corresponde al lugar infinito , veamos que multiplicidad tiene,

y sin usar bezout y con todos los teoremas anteriores, tenemos que si la multiplicidad es n entonces debe de haber n lugares en el divisor correspondiente a la linea porque $latex \partial(div(l_{PQ}))=0$


Tenemos que una curva elíptica es de la forma $latex y^2 = x^3 + \alpha x + \beta$

y $latex l_{PQ}$ es $latex y=mx+b$ por lo que si elevamos al cuadrado la linea e intersectamos con la curva

$latex (mx+b)^2 = x^3 + \alpha x + \beta$  es una cúbica en $latex x$ y en la homogenización tiene un cero de orden 3 en el punto al infinito $latex [1:0:1]$ el cual es el polo.

Eso quiere decir que si tenemos un polo de orden 3 , deben de haber 3 puntos donde choca la linea.
En símbolos:

La recta con pendiente distinta de 0 en la curva que pasa por P y Q:

$latex div(l_{PQ}/z) = (P)+(Q)+(R)-3\infty $

La recta que proyecta con el lugar infinito y R

$latex div(l_{R,\infty}/z)= R+(P+Q) -2\infty$

Por lo que:

$latex div(l_{PQ}/l_{R,\infty})=$ $latex div(l_{PQ}/z)-div(l_{R,\infty}/z)=(P)+(Q)-(P+Q)-\infty$

Por lo que de aquí sale la razón por la que está definida

Aquí vemos como se ven los divisores

Y de hecho, el grupo de Picard en este caso es isomorfo a los puntos de la curva bajo el mapeo:


$latex \Psi:C\rightarrow Pic^0(C)$
$latex P \mapsto P-\infty + Prin(\mathbb{F})$

Esto es inyectivo porque en género 1 con Riemann-Roch , ningún divisor $latex (P)-\infty$ es principal a menos que $latex P=\infty$


Espero les haya gustado

Eduardo Ruíz Duarte (beck)
twitter: @toorandom

Cohomología de de-Rham (parte 1 motivación desde análisis básico)

Aquí en mi blog he publicado cosas relacionadas con formas diferenciales, funciones alternantes, rotacionales, espacios tangentes, productos tensoriales de k-álgebras, de hecho construimos todas las funciones diferenciales en una variedad y vimos la derivada direccional como un funcional lineal y todo esto fue con álgebra, de hecho construimos un anillo en posts anteriores, por lo que ya estamos listos para poder definir un tema un poco más profundo, lo que haremos es examinar la cohomología de formas diferenciales.

Sabemos que una función continua real que está definida en un abierto de $latex \mathbb{R}$ tiene una función primitiva, es decir, se integra. Pero... ¿qué pasa con funciones multivariables? .

Para empezar vamos a restringirnos a funciones $latex C^{\infty}$ , es decir que tienen derivadas parciales continuas de todos los ordenes.

Con el propósito de saber por qué estamos examinando esta teoría , pongamos un ejemplo.

Sea $latex f:U\rightarrow \mathbb{R}^2$ diferenciable definida en un abierto de $latex \mathbb{R}^2$

Pregunta $latex \star$

¿Existe una función $latex F:U\rightarrow \mathbb{R}$ tal que:

* $latex \frac{\partial F}{\partial x_1}=f_1$  y   $latex \frac{\partial F}{\partial x_2}=f_2$  con $latex f=(f_1,f_2)$?

Sabemos que


$latex \frac{\partial^2 F}{\partial x_2 \partial x_1} = \frac{\partial^2 F}{\partial x_1\partial x_2}$

Por lo que deberíamos tener que

** $latex \frac{\partial f_1}{x_2}=\frac{\partial f_2}{x_1}$


Ahora, ¿existe $latex F$ suponiendo que $latex f=(f_1,f_2)$ satisface ** , ¿es esa condición de la igualdad suficiente?


Ejemplo:

Considera la función $latex f:\mathbb{R}^2 \rightarrow \mathbb{R}^2$ dada por:

$latex f(x_1,x_2) = \Big ( \frac{-x_2}{x_1^2+x_2^2} , \frac{x_1}{x_1^2+x_2^2} \Big )$


Como ejercicio puedes calcular las parciales de esa función y verás que en efecto se satisfacen las ecuaciones de ** , sin embargo no existe una función $latex F:\mathbb{R}^2-\lbrace 0 \rbrace \rightarrow \mathbb{R}$ que satisface *, y esto es fácil verlo, supongamos que sí existe, entonces:


$latex \int_{0}^{2\pi} \frac{d}{d\theta}F(cos\theta, sen\theta)d\theta = F(1,0)-F(1,0)=0$


Por otro lado, si desarrollamos el término de la integral con la regla de la cadena:

$latex \frac{d}{d\theta}F(cos\theta, sen\theta)$

$latex = \frac{\partial F}{\partial x}\cdot (-sen\theta) +\frac{\partial F}{\partial y}\cdot cos\theta$
$latex = -f_1(cos\theta,sen\theta)\cdot sen\theta + f_2(cos\theta, sen\theta)\cdot cos\theta = 1$

Esto es claro 1, sustituye y usa la $latex f$ original , por lo que la integral no puede ser 0 y esta contradicción significa que tal $latex F$ no existe.

Definición: Un subconjunto $latex X\subset \mathbb{R}^n$ se dice que es estrellado con respecto a un punto $latex x_0 \in X$ si el segmento $latex \lbrace tx_0 + (1-t)x \mid t\in [0,1]\rbrace$ está contenido en $latex X$ para todo $latex x\in X$

Teorema 1: Sea $latex U \subset \mathbb{R}^2$ un abierto estrellado, entonces para toda función diferenciable $latex (f_1,f_2):U\rightarrow \mathbb{R}^2$ que satisface **, tenemos que la pregunta $latex \star$ tiene solución.

La demostración es un poco de talacha, ya la hice y no es difícil, pero el punto es ver que el que se pueda definir la primitiva de una función depende de la topología del abierto $latex U$, esto no es coincidencia, podemos definir un invariante.


Por simplicidad y como esto es motivación para lo fuerte, seguiremos en $latex \mathbb{R}^2$.

Dado el abierto $latex U\subset \mathbb{R}^2$ y sea $latex C^{\infty}(U,\mathbb{R}^2)$ todas las funciones diferenciables $latex \phi:U\rightarrow \mathbb{R}^2$ , esto es uno de los primero ejemplos de espacios vectoriales de funciones, puedes demostrar que lo son bajo la suma usual y producto por escalares, puedes ver a la $latex \phi$ como un campo vectorial sobre $latex U$ (dibujando $latex \phi(u)$ con el punto $latex u\in U$.

Como lo habíamos definido antes en otro post, pero aquí en dimensión 2, tenemos el gradiente y rotacional:

$latex grad:C^{\infty}(U.\mathbb{R})\rightarrow C^{\infty}(U,\mathbb{R}^2)$
$latex grad(\phi)=\Big( \frac{\partial \phi}{\partial x_1},\frac{\partial \phi}{\partial x_2}\Big)$

 $latex rot:C^{\infty}(U.\mathbb{R}^{2})\rightarrow C^{\infty}(U,\mathbb{R})$

$latex rot(\phi_1,\phi_2)=\frac{\partial \phi_1}{\partial x_2} - \frac{\partial \phi_2}{\partial x_1}$

Aquí empieza lo interesante:


Nota que $latex rot \circ grad=0$, eso significa que el kernel del rotacional contiene a la imagen del gradiente .

Tenemos que el rotacional y gradiente son operadores lineales esto es que $latex Im(grad)$ es un subespacio de $latex Ker(rot)$, por lo que podemos hablar de el cociente de espacios vectoriales, es decir el espacio de clases $latex \alpha + Im(grad)$ donde $latex \alpha \in Ker(rot)$

***

$latex H^1(U)= Ker(rot)/Im(grad)$

Con esta definición podemos reformular el teorema 1

Teorema 1a: $latex U\subset \mathbb{R}^2 estrellado \Rightarrow H^1(U)=0$

Por otro lado , tenemos que el Ejemplo que desarrollamos $latex H^1(\mathbb{R}-\lbrace 0 \rbrace)\neq 0$.

De hecho se puede demostrar con un poco de cuidado que:

$latex H^1(\mathbb{R}^2 - \displaystyle \cup_{i=1}^k \lbrace x_i \rbrace) \cong \mathbb{R}^k$

De hecho... $latex k$ será el número de componentes conexas del espacio en cuestión, por lo que podemos decir que la dimensión de $latex H^1(U)$ es el número de hoyos en $latex U$

Podemos definir en analogía con *** a $latex H^0(U)=Ker(grad)$.

Lo anterior de los hoyos y eso es algo que suena muy importante por lo que realmente creo que debemos demostrarlo, y no es difícil, por lo que vamos a definir un criterio de conexidad para $latex U$

Teorema 2: Un abierto $latex U\subset \mathbb{R}^k$ es conexo $latex \Leftrightarrow$ $latex H^0(U)=\mathbb{R}$

Demostración:

Tenemos que $latex H^0(U)=Ker(grad)$. por lo que supón que tienes que $latex grad(f)=0$, esto implica que $latex f$ es localmente constante, o sea que todo $latex x_0 \in U$ tiene una vecindad $latex V(x_0)$ con $latex f(x)=f(x_0)$ cuando $latex x \in V(x_0)$ , si $latex U$ es conexo, entonces toda función localmente constante es constante, de hecho , si $latex x_0 \in U$ el conjunto:

$latex \lbrace x\in U\mid f(x)=f(x_0)\rbrace = f^{-1}(f(x_0))$

Es cerrado porque recuerden que $latex f$ es continuo, diferenciable, etcétera, también es abierto ya que $latex f$ es localmente constante, por lo que es igual a $latex U$ y $latex H^0(U)=\mathbb{R}$.

Para el regreso es más fácil ya que si $latex U$ no es conexo, entonces existe una función sobre
$latex f:U\rightarrow \lbrace 0,1 \rbrace$ tal que es localmente constante, entonces $latex grad(f)=0$ por lo que $latex dim H^0(U)>1$   $latex \blacksquare$

De hecho con lo que vimos anteriormente con el número de hoyos podrías extender esta demostración para decir que la dimensión es el número de componentes conexos.

En $latex \mathbb{R}^3$ las cosas son más interesantes.


En tres dimensiones tenemos el operador de divergencia que también lo habíamos construido en un post anterior, si extendemos $latex grad$ y $latex rot$ a $latex \mathbb{R}^3$ de manera natural y definimos

$latex div(f_1,f_2,f_3)=\frac{\partial f_1}{\partial x_1} + \frac{\partial f_2}{\partial x_2} + \frac{\partial f_3}{x_3}$

Podemos notar que aquí también sucede que $latex rot \circ grad = 0$ y adicionalmente que $latex div \circ rot=0$

Construimos de manera similar a $latex H^0(U)$ y $latex H^1(U)$ y definimos:

$latex H^2(U)=Ker(div)/Im(rot)$


Ya se imaginarán por donde voy los que han llevado un poco de topología algebraica,
el siguiente post será ya con complejos CW para ir aterrizando la idea.

saludos

Eduardo Ruíz Duarte (beck)
Twitter: @toorandom

Teorema de Riemann-Roch y divisores en criptografía, (Parte 2: Espacio proyectivo)

Como vimos anteriormente, lo que queremos es exprimir las propiedades de una curva algebraica a través de la geometría algebraica, en este caso de una curva elíptica o hiperelíptica.

Como lo mencioné al principio del post anterior, el grupo de una curva elíptica está fundamentado de manera "cochina" por (algunos) computólogos que implementan criptografía por el teorema de Bézout.

Siempre al definir una curva elíptica se define en su propiedad de grupo que un punto $latex (x,y)$ en la curva elíptica o hiperelíptica tiene como inverso a el punto $latex (x,-y)$ lo cual sucede al proyectarlo con un punto mágico que está en el infinito, esto es porque la curva elíptica realmente no vive en $latex \mathbb{R}^2$ como todos creen, realmente vive en otro espacio que es el que trataremos de explicar aquí, vive realmente en $latex \mathbb{P}^2_{\mathbb{C}}$, pronto veremos el por qué se les llama elípticas a través de otro nuevo espacio $latex \mathbb{C}/\Lambda$ y una función llamada $latex \wp$ de Weierstrass, pero eso aún está lejos de este post.

La respuesta elegante y limpia en vez de usar Bézout para justificar la estructura de grupo de una curva elíptica o hiperelíptica está a través del teorema de Riemann-Roch el cual trataremos de comprender a grandes rasgos, no olvides checar tu literatura

El teorema de Riemann-Roch une las propiedades algebraicas y topológicas de una curva, vamos a explorarlo un poco, aunque en esta primera parte del post definiremos primero lo que es el espacio proyectivo y algunas propiedades a través de ejemplos usando topología.

Como lo mencioné, vamos a hablar ahora del espacio proyectivo $latex \mathbb{P}^{n}_{\mathbb{K}}$, en el post anterior trabajamos en el espacio afín $latex \mathbb{A}^{n}_{\mathbb{K}}$ y definimos el campo de funciones, el cual jugará un papel imporante en Riemann-Roch

Recomiendo leer al menos la página de Wikipedia de geometría proyectiva así como el artículo del plano complejo proyectivo , aquí daré cierta intuición, ejemplos, definiciones y construcciones, para no dejar ese hueco.

Sea $latex V$ un espacio vectorial de dimensión finita sobre un campo $latex \mathbb{K}$ (de hecho para nuestros propósitos el espacio que tomaremos será $latex V=\mathbb{C}^2$) y considera la siguiente relación de equivalencia entre los vectores  $latex V\setminus \lbrace 0 \rbrace$:

$latex u\sim v \Leftrightarrow \exists \lambda \in \mathbb{K}^{*} \mid u=\lambda v$

Es decir, estamos diciendo que dos vectores $latex u$ y $latex v$ estarán en la misma partición (están relacionados) sí y sólo sí están en la misma linea que pasa por el origen, es decir, este espacio consta de todas las lineas que salen del origen bajo esta relación, con un ombligo, recuerda que quitamos al 0

Por lo que tenemos que si nuestro espacio vectorial  $latex V=\mathbb{C}^2$
$latex \mathbb{P}(V):=V\setminus \lbrace 0 \rbrace / \sim$

y para reducir notación:

$latex \mathbb{P}^{n}_{\mathbb{C}}:=\mathbb{P}(\mathbb{C}^{n+1})$

Por lo que a nosotros nos interesará trabajar en:

$latex \mathbb{P}^{2}_{\mathbb{C}}$

El cual es el plano proyectivo complejo.

Esta geometría realmente nace de la perspectiva a la hora de pintar un paisaje y quieres poder mostrar el horizonte en tu obra a pesar de que éste esté en el infinito.

De hecho, los puntos de $latex \mathbb{P}^{2}_{\mathbb{C}}$ son denotados como $latex [a:b:c]$

Ejemplo:

Como a mucha banda matemática y a mi, nos gustan los ejemplos para poder entender los conceptos abstractos, afortunadamente aquí sí hay algo en lo que todo el mundo es familiar.

Vamos a ver cómo se ve $latex \mathbb{P}^{1}_{\mathbb{R}}$, de hecho vamos a demostrar que este espacio es realmente homeomorfo al círculo $latex \mathbb{S}^1$

Este espacio se le llama linea proyectiva real y nace de considerar la relación de equivalencia mencionada inicialmente sobre $latex \mathbb{R}^2$.

Más formal:

Si $latex x,y\in \mathbb{R}^2$, tenemos que $latex x\sim y \Leftrightarrow x=\lambda y$ con $latex \lambda \in \mathbb{R}$ y:

$latex \mathbb{P}^{1}_{\mathbb{R}}=\mathbb{R}^2\setminus \lbrace 0 \rbrace / \sim$

Vamos a usar topología aquí para demostrar que $latex \mathbb{S}^1$ y $latex \mathbb{P}^{1}_{\mathbb{R}}$ son homeomorfos, de hecho la topología cociente aunque supongo que hay caminos tal vez más directos.

Consideremos:

$latex \psi:\mathbb{R}^2 \setminus \lbrace 0 \rbrace \rightarrow \mathbb{P}^1_{\mathbb{R}}$
$latex (x,y) \mapsto [x:y]$

Ahora, vamos a restringir esto a $latex \mathbb{S}^1$

es decir $latex \hat\psi = \psi\mid_{\mathbb{S}^1}$ por lo que tenemos que en $latex \hat\psi :\mathbb{S}^1 \rightarrow \mathbb{P}^1_{\mathbb{R}}$  $latex \hat\psi(x,y)=\hat\psi(-x,-y)$ es decir, a cada punto del círculo bajo la relación $latex \sim$ se reduce en la restricción al círculo a una relación más simple que le llamaremos $latex \hat\sim$ la cual definimos como $latex a,b\in \mathbb{S}^1$ entonces $latex a\hat\sim b\Leftrightarrow a=-b$

Es decir, la relación restringida al círculo nos dice que las antípodas están en la misma clase de equivalencia.

Entonces lo que basta demostrar es que $latex \tilde\psi:\mathbb{S}^1/\hat\sim \rightarrow \mathbb{S}^1$
es un homeomorfismo.

Consideremos el mapeo:

$latex \phi:\mathbb{S}^1 \rightarrow \mathbb{S}^1$

$latex (x,y) \mapsto (x^{2} - y^{2},2xy)$

Este mapeo está inspirado en $latex z\mapsto z^2$ en $latex \mathbb{C}$ pero viéndolo en $latex \mathbb{R}^2$ y restringido a $latex \mathbb{S}^1 \subset \mathbb{R}^2$

Este mapeo $latex \phi$ claramente es continuo y suprayectivo y $latex \phi$ pasa por el cociente bajo $latex \hat\sim$ o sea, respeta la relación de equivalencia $latex \hat\sim$ ya que si $latex z\in\mathbb{S}^1$ tenemos que $latex \phi(z)=\phi(-z) \Rightarrow z\hat\sim -z$

Usando la propiedad universal de la topología cociente con esta $latex \phi$ tenemos que $latex \tilde\psi:\mathbb{S}^1/\hat\sim \rightarrow \mathbb{S}^1$ es un homeomorfismo y es único.

Por lo que:

$latex \mathbb{P}^{1}_{\mathbb{R}}=\mathbb{R}^2\setminus \lbrace 0 \rbrace / \sim \cong \mathbb{S}^1$


Más ejemplos usuales existen , por ejemplo si nos tomamos $latex \mathbb{C}$ en vez de $latex \mathbb{R}$ ustedes pueden demostrar que la recta proyectiva compleja:

$latex \mathbb{P}^{1}_{\mathbb{C}} \cong \hat{\mathbb{C}}:=\mathbb{C}\cup \lbrace \infty \rbrace$

La cual es la esfera de Riemann, éste es un ejemplo fundamental en análisis complejo y geometría algebraica por ser una superficie de Riemann compacta, esto último es relevante ya que nos permite verla como una curva proyectiva algebraica.

Los espacios proyectivos complejos son una herramienta muy poderosa, ya que al agregar este punto $latex \infty$ en ciertos casos se puede definir la división por 0 haciendo que por ejemplo cualquier función racional meromorfa en los complejos sea extendida a una función continua sobre la la recta proyectiva compleja, mapeando sus polos al infinito y conservando continuidad.

En los espacios proyectivos suceden cosas interesantes, por ejemplo veremos que por la naturaleza del espacio en función de su relación de equivalencia, las ecuaciones algebraicas dentro de nuestro espacio proyectivo deberán ser homogéneas, o que existen un puntos que no están en el espacio vectorial en correspondencia con el proyectivo o que si definimos dos rectas paralelas en el espacio vectorial y lo transladamos al espacio proyectivo sí se intersectarán, de hecho TODAS las rectas del espacio proyectivo se intersectan en un punto 

Regresando a la analogía de las obras de pintura de paisajes, imagina ¿cómo pintarías la foto de unas vías del tren vistas de frente?, si observas bien las vías, éstas, pareciera que se intersectan en el horizonte.

Para terminar esto veamos lo que mencioné en negritas el penúltimo parrafo a éste.

Consideremos las soluciones (el conjunto de ceros) de un polinomio definido con sus variables en $latex \mathbb{P}^{n}_{\mathbb{K}}$ es decir, un punto en general sería con $latex n+1$ variables , $latex P=[x_0:...x_n]\in \mathbb{P}^{n}_{\mathbb{K}}$, estos puntos por como está definido el espacio proyectivo, están determinados por la multiplicación por un escalar $latex \lambda$, el cual da la relación de equivalencia, por lo que un polinomio con variables proyectivas deberán considerar esa restricción a la hora de considerar sus soluciones, estos polinomios se les llama homogéneos

Definición (polinomio homogéneo): Un polinomio:

$latex f(x_0,x_1,...,x_n) = \displaystyle \sum { a_{\eta_0...\eta_n}}x_{0}^{\eta_0}...x_{n}^{\eta_n}$

Se dice homogeneo de grado $latex d$ si TODOS sus monomios tienen el mismo grado $latex d=\sum_{i=0}^{n} \eta_i$

Por lo que si $latex f$ es homogéneo de grado $latex d$ entonces:

$latex f(\lambda x_0, ..., \lambda x_n)=\lambda^d f(x_0,...,x_n)$

Con esto tenemos que los polinomios homogéneos están bien definidos en el espacio proyectivo.

Ahora, lo que nos resta ver es una propiedad interesante, dos lineas siempre se intersectan en el plano proyectivo, y para esto lo que haremos un ejemplo, será transformar polinomios en dos variables complejas $latex \mathbb{C}^2$ a polinomios en $latex \mathbb{P}^2_{\mathbb{C}}$ a través de un proceso que se llama "homogenización" , y lo haremos con dos lineas paralelas, y veremos como es la intersección de sus imágenes.

La siguiente definición es para construir un polinomio cualquiera, a un polinomio homogéneo , es decir con monomios del mismo grado, esta operación es invertible.

Definición (homogeinización): Sea $latex p(x,y) \in \mathbb{C}[x,y]$, el polinomio correspondiente en $latex \mathbb{P}^2_{\mathbb{C}}$ es:

$latex p(x,y,z)=z^{n}p(\frac{x}{z},\frac{y}{z})$

Es fácil ver que el polinomio resultante de este proceso es realmente homogéneo.

Ejemplo (intersección de las imágenes bajo homogenización de dos rectas afines):

Sean
$latex x+y=2$
$latex x+y=3$

dos rectas definidas en $latex \mathbb{C}^2$

claramente son paralelas, homogeneizando tenemos que

$latex x+y=2z$
$latex x+y=3z$

por lo que tenemos que $latex [a:-a:0] \in \mathbb{P}^2_{\mathbb{C}}$ está en la linea al infinito y es solución de ambas ecuaciones,

nota que $latex [0:0:0]$ también es solución, pero éste punto no está definido en el espacio proyectivo por construcción.

Otro ejemplo serían dos circunferencias de radio distinto:


$latex x^2 + y^2 = 1$
$latex x^2 + y^2 = 2$

Claramente no se intersectan en el espacio afín complejo

Homogeneizando, tenemos que

$latex x^2 + y^2 -1 \mapsto z^2\Big ( \frac{x^2}{z^2}+\frac{y^2}{z^2}-1\Big )=x^2+y^2-z^2$

Similarmente con el otro polinomio, por lo que tenemos que intersectar en $latex \mathbb{P}^2_{\mathbb{C}}$

$latex x^2+y^2-z^2$   y   $latex x^2+y^2-2z^2$

y tenemos que todos los puntos de la forma $latex \lambda(\pm 1,\pm i,0)$ son soluciones, y si $latex \lambda \neq 0$

tenemos que $latex [\pm 1:\pm i:0]\in \mathbb{P}^2_{\mathbb{C}}$ es un punto en la linea al infinito que intersecta a ambas circunferencias proyectivas de distinto radio.

La relación con curvas elípticas será que éstas realmente hay que proyectivizarlas (homogeneizarlas) y al trabajar con ellas en criptografía es viéndolas en el espacio proyectivo, es decir para que todo funcione como queremos necesitamos la cerradura proyectiva, mas no el hecho de usar un punto cualquiera para darle estructura de grupo.


Con esto, y el post anterior estamos listos para la siguiente parte que será el teorema de Riemann-Roch


Eduardo Ruiz Duarte (beck)
twitter: @toorandom

Teorema de Riemann-Roch y divisores en criptografía (Parte 1: campos de funciones y gavillas sobre variedades)

En criptografía muchos han visto que se estudian las curvas elípticas y menos frecuentemente las curvas hiperelípticas, algunos recordarán la estructura de grupo que se le da a una curva elíptica $latex C$ con la usual regla de intersección de una recta con la curva haciendo uso abusivo del teorema de Bézout para fundamentar la estructura de grupo que hay en sus puntos, que más formalmente, es la estructura de grupo que hay en las clases de divisores formados por las sumas formales de ideales máximos de todos los subanillos del campo de funciones de $latex \mathbb{K}(C)$, este grupo es el grupo de Picard de orden 0 de la curva $latex C$ que es:

 $latex Pic^0(C) = Div^0(C)/Prin(C) \cong \mathbb{J}(C)$.

Esta manera de ver las cosas NO es para complicar lo ya existente, sino es con propósitos de poder exprimir más la teoría que lo respalda para poder investigarlo mejor y generalizarlo a otras curvas no elípticas.

La estructura de grupo de manera inocente o usual se puede ver en muchos textos pobres en matemáticas pero tal vez ricos en aplicaciones criptográficas como esto:

El propósito de este post será el poder resumirte la teoría que hay detrás.


Comencemos con unas definiciones, voy a suponer que quien me lee está familiarizado con la topología de Zariski la cual está definida por los conjuntos algebraicos como cerrados, de hecho estas definiciones son las interesantes para la topología de Zariski, y con esto pueden demostrar fácilmente las propiedades de espacio topológico.

Definición (ceros):
Sea $latex A:= \mathbb{K}[x_1,...,x_n]$ el anillo de polinomios en $latex n$ variables sobre el campo algebraicamente cerrado $latex \mathbb{K}$ y $latex J \subset \mathbb{K}[x_1,...,x_n]$ un ideal, entonces definimos el conjunto de ceros del ideal $latex J$ como:

$latex V(J):=\lbrace P\in \mathbb{A}^{n}_{\mathbb{K}} \mid f(P)=0$     $latex \forall f\in J\rbrace$


Definición (variedad afín): Un subconjunto $latex X\subset \mathbb{A}^n_{\mathbb{K}}$ es un conjunto algebraico (variedad afín) en el espacio afín $latex \mathbb{A}^n_{\mathbb{K}}$ si existe un $latex T\subset \mathbb{K}[x_1,...,x_n]$ tal que:

$latex X=V(T)$

Decimos que $latex X$ es un cerrado de Zariski, en la topología dada a  $latex \mathbb{A}^n_{\mathbb{K}}$.

Veámos primero lo que es el anillo de coordenadas de una variedad.

Definición (función polinomial en la variedad V): Una función polinomial es un mapeo $latex f:V \rightarrow \mathbb{K}$ tal que existe un $latex F\in \mathbb{K}[x_1,...,x_n]$ con $latex f(P)=F(P)$  $latex \forall P\in V$

Este polinomio $latex F$ no está únicamente determinado por los valores que toma en $latex V$ o sea si tenemos $latex F,G\in \mathbb{K}[x_1,...,x_n]$:


$latex F\mid_{V}=G\mid_{V} \Leftrightarrow (F-G)\mid_{V}=0 \Leftrightarrow F-G\in I(V)$

Donde:

$latex I(V):=\lbrace f\in \mathbb{K}[x_1,...,x_n] \mid f(P)=0$    $latex \forall P\in V\rbrace$



Esta definición de función polinomial y su relación de igualdad con otros polinomios, huele a una relación de equivalencia, por lo que vamos a suponer que lo es y se deja a quien lee para que lo demuestre y tenemos que:

Denotaremos ahora a $latex V$ como el conjunto algebraico $latex V(I)$ donde $latex I$ es ideal de $latex \mathbb{K}[x_1,...,x_n]$

Definición (anillo de coordenadas de una variedad): Un anillo de coordenadas de una variedad $latex V$ es:

$latex \mathbb{K}[V]:=\mathbb{K}[x_1,...,x_n]/I(V)$

Este anillo sabemos que es un dominio entero si $latex I(V)$ es un ideal primo, y esto naturalmente sucede si $latex V$ es irreducible , es decir no es union de otros cerrados de zariski


De lo anterior sobre funciones polinomiales y la última definición se puede demostrar que:

$latex K[V]=\lbrace f \mid f:V\rightarrow \mathbb{K}$ es una función polinomial $latex \rbrace$

Cabe notar que se le llama anillo de coordenadas porque las funciones que te dan la i-ésima coordenada de los elementos de $latex V$, $latex x_i$ son las generadoras de $latex \mathbb{K}[V]$

Es fácil ver que $latex \mathbb{K}[ \mathbb{A}^n_{\mathbb{K}}]=\mathbb{K}[x_1,...,x_n]$ y que el anillo $latex \mathbb{K}[V]$ juega el papel para $latex V$ como $latex \mathbb{K}[x_1,...,x_n]$ para $latex \mathbb{A}^n_{\mathbb{K}}$

Observaciónes sobre lo anterior con respecto a la topología de Zariski en $latex \mathbb{A}^n_{\mathbb{K}}$.

• Los ideales primos de $latex \mathbb{K}[V]$ están en correspondencia 1:1 con irreducibles $latex W\subset V$
• Los ideales máximos de  $latex \mathbb{K}[V]$ están en correspondencia 1:1 con los puntos de $latex V$
• Los ideales radicales de $latex \mathbb{K}[V]$ están en correspondencia 1:1 con los cerrados $latex W\subset V$

Definición (campo de funciones de V): El campo de funciones de $latex V$ es el campo de fracciones de $latex \mathbb{K}[V]$ y es denotado por $latex \mathbb{K}(V)$, las $latex f\in \mathbb{K}(V)$ se llaman funciones racionales sobre $latex V$

Definición (función regular en P): Una función $latex f\in \mathbb{K}(V)$ y $latex P\in V$ se dice que es regular en $latex P$ si $latex f=\frac{g}{h}$ con $latex h(P)\neq 0$, y definimos:

$latex dom(f):=\lbrace P\in V \mid f$ es regular en $latex P\rbrace$

Proposición: El conjunto:

$latex V_f:=\lbrace P\in V\mid f(P)\neq 0\rbrace$

es un abierto de $latex V$


Teorema: 

• $latex dom(f)$ es abierto y denso en $latex V$
• $latex dom(f)=V\Leftrightarrow f\in \mathbb{K}[V]$
• $latex V_g\subset dom(f) \Leftrightarrow f\in \mathbb{K}[V][1/g]$

Ahora, entraremos a un concepto central, para poder analizar una variedad localmente... para esto sabemos que un anillo local sólo tienen un ideal máximo, y tenemos que la siguiente definición

Definición (anillo de funciones regulares): El anillo de funciones regulares de $latex V$ localizado en el punto $latex P\in V$ es:

$latex O_{V,P}:=\lbrace f\in \mathbb{K}(V)\mid f$ es regular en $latex P\rbrace$

Es fácil demostrar que esto es en efecto un subanillo de $latex  \mathbb{K}(V)$ y que su único ideal máximo no deberá tener unidades por lo que su ideal máximo es:

$latex m_{P}:=\lbrace f/g \in \mathbb{K}(V)\mid f(P)=0, g(P)\neq 0 \rbrace$

Ahora vamos a la últma parte de este blog donde discutiremos la estructura de gavilla de una variedad

Estructura de gavilla de una variedad

Tenemos que el anillo $latex O_{V,P}$ es local y es un subanillo de $latex \mathbb{K}(V)$ y su ideal máximo es $latex m_{P}$, es fácil relacionar a $latex O_{V,P}$ con $latex \mathbb{K}[V]$ ya que con localización puedes demostrar que:

$latex \hat{m}_P=\lbrace f\in \mathbb{K}[V]\mid f(P)=0\rbrace=I(\lbrace P \rbrace)+I(V)\subset \mathbb{K}[V]$

Es máximo y:

$latex O_{V,P}=\mathbb{K}[V]_{\hat{m}_P}$


Es decir que $latex O_{V,P}$ es la localización del anillo de coordenadas de $latex V$ en el ideal máximo $latex \hat{m}_P$

Ahora vamos a definir el concepto final:

Definición-Teorema (estructura de gavilla en $latex O_{V}(U)$, germen y fibra ): Para todo abierto $latex U \subset V$ tenemos:

$latex O(U):=O_{V}(U):=\lbrace f\in \mathbb{K}(V) \mid f$ es regular en $latex U \rbrace$

Es una $latex \mathbb{K}-$álgebra con $latex O_{V}(\emptyset):=\lbrace 0 \rbrace$

Todos los $latex O_{V}(U)$ con $latex U\subset V$ forman una gavilla $latex O_V$ bajo la restricción de homomorfismos usual y el anillo $latex O_{V,P}$ es una fibra de la gavilla $latex O_V$  y los elementos $latex f\in O_{V,P}$ se les llama gérmenes de funciones y:

$latex O(V)=\mathbb{K}[V]$


La teoría de gavillas da una estructura rica a una variedad, en este caso , puede ser el de una curva elíptica o hiperelíptica

Saludos

Eduardo Ruiz Duarte (beck)
Twitter: @toorandom

Criptografía asimétrica combinatoria-algebraica no usual con bases de Gröbner

Siempre me ha gustado investigar estructuras algebraicas con el fin de poder ver si puedo sumergir criptografía asimétrica dura ahí, generalmente ésta basada en el problema de logaritmo discreto en curvas algebraicas; considero que es mi área favorita de trabajo y posiblemente a lo que me vaya a dedicar el resto de mi vida, pero aquí vamos a ver algo diferente que podría o no ser seguro en su implementación pero no deja de ser interesante.


Primero vamos a analizar un caso particular de un esquema de cifrado con polinomios y luego veremos cómo generalizarlo y definiendo con bases de Gröbner.

Vamos a utilizar cualquier $latex \mathbb{F}-algebra$ de tipo finito, i.e. finitamente generada, con grado de trascendencia $latex n$ veamos cómo funciona esto.

Construcción del algoritmo de cifrado:

Sea $latex \mathbb{F}$ un campo finito y $latex T=\lbrace t_{i}\rbrace_{i=1}^{n}$ un conjunto de variables.


Queremos que $latex A$ reciba un mensaje $latex m\in \mathbb{F}$ de $latex B$ cifrado.

• $latex A$ va a escoger un vector aleatorio $latex y\in \mathbb{F}^{n}$ como llave privada

• $latex A$ escoge polinomios como llave pública $latex P=\lbrace q_j \rbrace \subseteq \mathbb{F}[T]$ tal que $latex q_j(y)=0$ $latex \forall j$

         Es fácil generar polinomios con los ceros que necesitamos, por ejemplo si
         ya tenemos la llave privada $latex y$ tomas $latex q_j = \hat {q}_j - \hat{q}_j(y)$ con $latex \hat{q}_j \in \mathbb{F}[T]$.
         Lo que no es tan fácil es escogerlos seguros y álgebraicamente independientes, pero hay métodos.

•  $latex B$ quiere mandar el mensaje $latex m\in \mathbb{F}$ a $latex A$ por lo que se toma un elemento del ideal generado por la llave pública $latex P$ que es $latex (P) \subset \mathbb{F}[T]$:

   $latex p = \displaystyle \sum { h_j q_j } $

En otras palabras escoge $latex \lbrace h_j \rbrace \subset \mathbb{F}[T]$ y genera el polinomio $latex p$

• $latex B$ le manda a $latex A$ el polinomio multivariable        

$latex c=p+m$


Este esquema de cifrado funciona ya que $latex A$ va a poder obtener $latex m\in \mathbb{F}$ ya que conoce los ceros de los generadores del ideal $latex (P)\in \mathbb{F}[T]$ por lo tanto conoce los ceros de $latex p$ independientemente de los $latex \lbrace h_j \rbrace$ , por lo que usando su llave privada $latex y$ tenemos que $latex A$ puede calcular fácilmente

$latex c(y)=p(y)+m=m$


Nota que este esquema de cifrado es probabilístico y no determinístico, i.e. en cada
ocasión que se cifra $latex m$ es diferente ya que depende de los elementos del ideal de la llave pública que se tomen.

Su seguridad también depende de los ceros del conjunto algebraico generado por $latex B$, en este caso cada cero sería $latex y=(y_1,y_2,...,y_n)$ y cualquier cero en la intersección de las hipersuperficies funcionaría, su seguridad depende de la solución de sistemas de ecuaciones algebraicos no lineales de grado arbitrario , es decir, en dimensión grande y con un número grande de polinomios generadores independientes del ideal de la llave pública, es POSIBLE tener criptografía segura, digo posible porque no se ha demostrado que su solución NO sea en tiempo polinomial, pero creo que podría ser más seguro si usamos la teoría de bases de Gröbner.

Generalización:

Veamos unas definiciones que vienen de la teoría de bases de Gröbner para poder intentar una generalización, las cuales incluyen la reducción módulo otro polinomio multivariable, donde los monomios deberán estar ordenados bajo cierto orden lexicográfico.

Definición (módulo polinomio multivariable): Decimos que $latex f$ reduce a $latex h$ módulo $latex g$ parcialmente si $latex a_{i}X^{i}$ es un monomio de $latex f$ que es divisible por el término líder de $latex g$ ,$latex lt(g)$ (líder bajo el órden con el que organicemos nuestros polinomios como el lexicográfico por grado) y que sucede que:

$latex h=f-\frac{a_{i}X^{i}}{lt(g)}g$

Donde escribimos que $latex f \equiv h \bmod g$

Definición (módulo un conjunto de polinomios): Sea $latex G=\lbrace g_1,...,g_l \rbrace \subset \mathbb{F}[T]$ y sea $latex f\in \mathbb{F}[T]$, entonces decimos que $latex f$ se reduce a $latex h$ módulo $latex G$ ($latex f \equiv h \bmod G$) si tenemos la sucesión $latex h_0=f, ..., h_k=h$ tal que $latex h_j \equiv h_{j+1} \bmod g$ para algún $latex g\in G$

Definición (base de Gröbner): Sea $latex F=\lbrace g_1, ..., g_l \rbrace \subset \mathbb{F}[T]$ un conjunto finito de polinomios en $latex m=|T|$ variables e $latex I\subset \mathbb{F}[T]$ el ideal generado por $latex F$, decimos que $latex F$ es una base de Gröbner para el ideal $latex I$ si para todo $latex 0\neq f\in I$ se tiene que $latex lt(g_k)\mid lt(f)$ para algún $latex g_k\in F$


Teorema: F es una base de Gröbner para un ideal $latex I\subset \mathbb{F}[T]$ $latex \Leftrightarrow$ $latex \forall f \in I$ $latex f\equiv 0 \bmod F$

Con este último teorema nos resulta TRIVIAL el poder construir ideales aleatorios (finitos, anillos noetherianos) y su base de Gröbner asociada.

Regresando al esquema de cifrado original y rehaciéndolo con esto:

$latex A$ escoge una base de Gröbner $latex G=\lbrace g_1,...,g_l\rbrace$ de un ideal $latex I \subset \mathbb{F}[T]$, la llave privada de $latex A$ es $latex G$.

Sea $latex S\subset \mathbb{F}[T]$ el conjunto de TODOS los polinomios que no pueden ser reducidos módulo $latex G$ (ve las definiciones anteriores), este $latex S$ realmente sería el conjunto de representantes del anillo $latex \mathbb{F}[T]/I$ como ya se lo habrán imaginado, ahora supón que $latex S$ es público, aunque $latex G$ no lo sea, tenemos que todo mensaje $latex m \in \mathbb{F}$ es un elemento de $latex S$.

Un ejemplo:


 Sea $latex T=\lbrace t_1,...,t_n\rbrace$ y $latex y \in \mathbb{F}^n$ un punto secreto, $latex A$ toma como base de gröbner $latex G=\lbrace t_1-y_1, ..., t_n - y_n\rbrace$  en este caso tenemos que $latex S=\mathbb{F}[T]/(G)\cong \mathbb{F}$ es el campo de las constantes.

Ahora $latex A$ escoge un conjunto como llave pública $latex P=\lbrace q_j \rbrace \subset I=(G)$, esto es fácil ya que  podría tomar un $latex \hat{q}_j\in \mathbb{F}[T]$ arbitrario y calcular $latex q_j = \hat{q}_j - \overline{q}_j$ donde $latex \overline{q}_j \in S$ y $latex \hat{q}_j \equiv \overline{q}_j \bmod G$

Consideremos el ideal $latex J=(P)$ y $latex m\in S$, entonces $latex B$ le cifrará a $latex A$ el mensaje $latex m$ escogiendo al azar un elemento de $latex J$, ya que la llave pública de $latex A$ es $latex P$ y $latex J=(P)$:

$latex p=\displaystyle \sum h_{j}q{j} \in J$

$latex B$ le manda a $latex A$ $latex c=p+m$

$latex A$ al recibir $latex c$ sólo tendría que reducirlo módulo la base de Gröbner $latex G$ 

En este ejemplo cuando $latex G=\lbrace t_i - y_i \rbrace$ sería el caso particular que vimos en el principio.


Esta criptografía es rara y no es usada ni considerada AÚN SEGURA debido a que falta demostrar que tan dificil es el problema en términos de complejidad.


Espero les haya gustado

Eduardo Ruíz Duarte (beck)
@toorandom

Hice programa para simular evolución de organismos libre, licencia MIT, simulacion genetica con bases nitrogenadas y estructura similar a una celula

Hice un algoritmo evolutivo que la simple lectura de su código posiblemente te hará entender los fundamentos de la teoría de darwin y su selección natural, así como los fundamentos de reproducción celular y herencia es un api pero trae un demo, uso bases nitrogenadas reales complementarias y células con una estructura similar a un organismo (con respecto a su núcleo y material genético).

La reproducción se da entre los más aptos random en el universo de población con distribución uniforme bajo el producto de sus aptitudes con respecto a un gen elite.

La manera de que estos se juntan es si son más aptos, esto es para simular el elitismo biologico, podrian reproducirse otros no aptos con cierta probabilidad .

Sus hijos comparten aproximadamente la mitad de los genes de sus padres.

Las poblaciones envejecen en cada generación, dañando el ADN en cierto porcentaje de los menos aptos.


Corranlo... trae un demo y me dicen que opinan... segun yo quedo muy didactico.

Y se puede adaptar para usar genomas reales y trazar evolucion no solo de 1 gen sino de varios a la vez.

En mi programa una celula humana ocuparía aproximadamente 9gb de memoria (46 cromosomas, 30 mil genes en el ADN con 1000 pares de bases nitrogenadas)

Por lo que en el demo uso un organismo con 4 cromosomas pero pueden bajar los genomas de ECOLI que ocupan como 6 mb en mi programa y generar poblaciones para ver como evolucionan... aqui tengo uno.

http://math.co.ro/ecoli.dna

Gracias Ximena Tochtli Bouchain Pedrón
por resolverme dudas de genética y reproducción celular, ya que con sus tips y consejos esto funciona y es más realista :)

Esta aquí el leeme y el código
http://b3ck.blogspot.mx
Salu2

Eduardo Ruiz (beck)


Aquí dejo el LEEME.TXT

bevolucion-0.1.tar.gz

Copyright Nov-2013 Eduardo Ruiz Duarte (rduarte@ciencias.unam.mx)


Programa para calcular las generaciones requeridas para alcanzar la estructura de un gen definida
utilizando la estructura aproximada biologica de un organismo.

Si quieres aprender un poco de genetica basica fundamental, sigue leyendo y corre este programa

Si quieres aprender mas de la parte biologica, quien me asesoro fue Ximena Tochtli Bouchain, escribele a rhapanus@gmail.com

Si quieres saber como funciona el API , lee los prototipos y sus comentarios al final del header bevolucion.h

Si estas desesperado y te da flojera leer esto , solo compila y corre el programa que ya trae un DEMO

./compila
./bevolucion


en el ejemplo se intenta evolucionar a un gen_elite aleatorio.



COMO FUNCIONA?

Se puede definir.
numero de organismos
numero de cromosomas
numero de genes
numero de pares de bases nitrogenadas por gen
coeficiente de mutacion (cuantos pares de bases se van a modificar aleatoriamente en todos los genes... podrian no modificarse algunos genes por probabilidad)
cromosoma y gen de referencia para analizar su evolucion

QUE HAY EN EL DEMO? [ main() ]

En el main() se implementa:

 INICIO_ALGORITMO {

1. El programa genera una poblacion con genes aleatorios y un gen_elite para comparar la evolucion, cada organismo contiene en su 'ser'
  su coeficiente de adaptacion con respecto al gen_elite

  LOOP() {
2. Se organizan jerarquicamente en funcion de su adaptacion al gen_elite

3. Usando la distribucion aleatoria uniforme escogemos aleatoriamente 2 padres aptos para reproducirse (de acuerdo a su coeficiente de adaptacion)
  podrian no ser los mas aptos, pero la funcion esta probada para arrojar mayormente aptos al azar.
  para simular elitismo usual entre organismos.

4. Se reproducen y generan un hijo con cierta probabilidad de mutacion y se le integra en su 'ser' su coeficiente de adaptacion
  el ADN de el hijo contiene genes con 50% de probabilidad del padre y 50% de probabilidad de la madre

5. Se integra a la poblacion si este hijo es mas apto que el menos apto

6. Muere el menos apto

7. Envejece 1/3 de la poblacion menos adaptada de manera que se dania el ADN,  el danio es una mutacion
  de solo 1 par de bases nitrogenadas en el gen de referencia.
  Esto esta fundamentado en que el envejecimiento consiste en la creacion de proteinas menos adecuadas
  para el ciclo de vida de las celulas debido a que el ADN contiene ya informacion erronea
  (el ADN contiene las 'instrucciones' del ciclo de vida de una celula, creacion de proteinas)
  Por ejemplo los rayos UV danian el gen XPD humano que llevan a defectos en la reparacion del ADN y transcripccion.
  las personas con este danio tienen el sindrome de Cockayne, por eso aqui modelamos con 1/3 de los menos
  adaptados la mutacion en el gen de referencia.

 }
}
FIN_ALGORITMO


Cada organismo (celula) esta organizada asi:

typedef struct celula_s
{
  cromosoma cromosomas[MAX_CROMOSOMAS];
  int16_t num_cromo;
  int16_t num_genes;
  int32_t aptitud_gen_ref;
  uint64_t identidad;
  uint32_t padre, madre;
  int32_t num_hijos;
  int32_t hijos[MAX_HIJOS];
 } celula;

donde su 'identidad' esta compuesta de 64 bits
{20 bits info de padre}{20 bits info de madre}{4 bits pseudo-random}{20 bits (Padre XOR Madre) + num_hijos_padre+num_hijos_madre}


Las variables globales gGen_ref y gCromo_ref son para encontrar el gen de referencia para evolucionar, esta definida en main() y se genera aleatoriamente ej. (ATCGGCTA)


Todas las subestructuras estan organizadas jerarquicamente con los componentes biologicos del organismo simple (solo nucleo)


CROMOSOMA:
Un cromosoma tiene el ADN enrollado y tiene asociadas proteinas, especialmente histonas, aqui las podemos relacionar con el mismo indice
pero la estructura de proteinas que el cuerpo usa para unir el ADN como cromatina no se usa aun en esta implementacion aun (ni otras proteinas)

typedef struct cromosoma_s
{
adn molecula_adn;
uint64_t proteinas[MAX_GENES * MAX_NUC_GEN];
} cromosoma;

ADN:
El ADN esta seccionado por genes
typedef struct adn_s
{
gen genes[MAX_GENES];
int8_t recesivo;
} adn;

GEN:
Un Gen esta compuesto de bases nitrogenadas, y guardaremos su aptitud y tamanio de pares de bases nitrogenadas en format AT,TA,GC,CG,AU,UA
que son los pares complementarios de pirimidinas y purinas en el ADN de un organismo y en ARN (U:=Uracilo que sustituye T=Timina)

typedef struct gen_s
{
  uint8_t par_bases[MAX_NUC_GEN];
  uint16_t tamano;
  uint32_t aptitud;
} gen;


PAR DE BASES NITROGENADAS

#define Adenina     0x08
#define Citosina    0x04
#define Guanina     0x02
#define Timina      0x01
#define Uracilo     0x0f
 ADN pares complementarios
#define AT (int8_t)(Adenina<<4 imina="" p="">#define TA (int8_t)(Timina<<4 denina="" p="">#define GC (int8_t)(Guanina<<4 itosina="" p="">#define CG (int8_t)(Citosina<<4 p="" uanina=""> ARN pares complementarios
#define AU (int8_t)(Adenina<<4 p="" racilo="">#define UA (int8_t)(Uracilo<<4 denina="" p="">

Integración motívica

Existe toda una teoría motívica de integración para cada variedad compleja suave, y esto sirve para la nueva teoría de cuerdas, la teoría motívica fue introducida por Kontsevich en 1995, donde anunció una solución a la conjetura de Batyrev sobre 

dos variedades Calabi-Yau birracionalmente equivalentes tienen los mismos números de Hodge.

Esta conjetura motivó el trabajo en física teórica ya mencionado sobre teoría de cuerdas, donde se cree que el universo visto como una variedad  es localmente el producto de $latex \mathbb{R}^4$ (Minkowski) con un componente compacto (Una variedad de Calabi-Yau)

Aquí sólo resumiremos un artículo de Looijenga (Motivic Measures)  sobre como se debe interpretar la integral motívica, para poder medir volúmenes, o cualquier cosa en cualquier variedad, dimensión, et cétera.

recomiendo leer también What is motivic measure? de Hales, donde expone la aritmética motívica a detalle de J. Denef y F. Loeser, como aquí lo mencioné aquí veremos en resumen lo que es "Motivic Measures" de Looijenga.

La integración motívica toma valores en el anillo motívico $latex \mathbb{M}$ el cual a grandes rasgos tiene como elementos combinaciones $latex \mathbb{Z}$-lineales formales de variedades, con suma como la suma disjunta de variedades y multiplicación como el producto directo de éstas.

Este anillo no está ordenado.

Sea $latex \Omega \\$ una variedad compleja de dimensión $latex n \\$ y $latex \displaystyle \mathfrak{D}=\sum_{i=1}^{r}a_{i}\mathfrak{D}_{i}$ un divisor efectivo en $latex \Omega \\$ con cruces normales simples, la integral motívica del par $latex (\Omega,\mathfrak{D})$ es:

$latex \int_{J_{\infty}(\Omega)}F_{\mathfrak{D}}d_{\mu}=\displaystyle \sum_{J\subseteq \lbrace 1,...,r\rbrace} [\mathfrak{D}^{\circ}_{J}]\cdot \Big (\prod_{j\in J} \frac{\mathbb{L}-1}{\mathbb{L}^{a_{j}+1}-1}\cdot \mathbb{L}^{-n} \Big )$ 

Aquí el espacio de arcos formales de $latex \Omega \\$ es $latex J_\infty(\Omega)$ , aquí también $latex F_{\mathfrak{D}$ es una función definida en $latex J_\infty(\Omega)$, la integral motívica de $latex (\Omega, \mathfrak{D})$ es la integral de $latex F_{\mathfrak{D}$ sobre $latex J_\infty(\Omega)$ respecto a una medida $latex \mu \\$ en $latex J_\infty(\Omega)$, esta medida toma valores en $latex \mathbb{M} $

Los arcos formales $latex J_\infty(\Omega)$ están definidos fijando una variedad compleja $latex \Omega \\$ , los puntos de este espacio corresponden a "arcos formales" , imagina una curva infinitesimal centrada en un punto de $latex \Omega \\ $, eso es un punto con una dirección  tangente en ese punto, una dirección tangente de segundo orden, de tercer orden, et cétera... por eso se puede "intuir" que $latex J_\infty(\Omega)$ es un haz afín infinidimensional sobre $latex \Omega \\$.

$latex \mathbb{L}$ es la línea afín en $latex \mathbb{M}$

Espacios tangente y derivaciones

Ya vimos cómo funcionan las k-formas diferenciales y de hecho construímos con ellas el rotacional, divergencia y gradiente, vamos ahora a construir el espacio tangente, como repito, esto es con el fin de poder entender qué sucede en la topología de Zariski a la hora de definir el espacio tangente allí y usar las herramientas de geometría diferencial en geometría algebraica para el cálculo de singularidades, ahora lo haremos en $latex \mathbb{R}^n$ después esto se podrá dar el salgo a geometría algebraica para definirlo en $latex \mathbb{A}^{n}_{\mathbb{K}$ o en $latex \mathbb{P}^{n}_{\mathbb{K}$ , todo esto es para después definir orientación lo cual es un tema a mi gusto un poco complicado, pero es necesario para saber la "dirección" de la derivada y cómo se comportan los campos vectoriales.

Estoy suponiendo que el lector conoce lo que es una variedad (diferenciable) en $latex \mathbb{R}^n$, si no lo conoce, de manera rápida, una variedad de dimensión n es un espacio topológico en el cual para todo punto de éste existe un abierto al cual pertenece ese punto, y ese abierto es homeomorfo a $latex \mathbb{R}^n$, esta variedad es diferenciable si no tiene autointersecciones, picos, etcétera .

Recuerden cuando hace muchos años quemaban a los físicos por decir que la tierra era esférica, donde como siempre, la iglesia decía que eran unos blasfemos porque ellos afirmaban que era plana, bueno... esto es porque la tierra es localmente euclídea (una variedad) , es decir... es homeomorfa a la esfera de dimensión 2     $latex \mathbb{S}^2$ por lo que los religiosos por verla localmente euclídea pensaban que su forma era de $latex \mathbb{R}^2$ .
(ver la definición de variedad diferenciable y variedad en otro recurso en línea si así no te quedó claro antes de continuar).

Definición: Un mapeo suave $latex \gamma : [a,b] \rightarrow M$ de un intervalo a una subvariedad diferenciable $latex M \subset \mathbb{R}^n$ es una curva suave en $latex M \\$


Definición: Sea $latex M \subset \mathbb{R}^n$ una variedad diferenciable, y $latex p \in M$.
Un vector $latex v \\$ es un vector tangente a $latex M \\$ en $latex p$ si existe una curva suave $latex \gamma_{p}:[-\epsilon,\epsilon]\rightarrow M$ que pase por $latex p =\gamma_{p}(0)$  tal que $latex v=\gamma_{p}\prime (0)$, El espacio tangente $latex T_{p}M$ de $latex M \\$ en $latex p \\$ es el conjunto de todos los vectores tangentes a $latex M \\$ en $latex p \\$

Teorema:
Sea $latex M \\ $ una variedad en $latex \mathbb{R}^n$ de dimensión k, entonces tenemos que  $latex \forall p \in M$ existe un abierto $latex U \ni p$  tal que $latex M \\$ está definida en $latex U \\$ como la solución de un sistema de $latex (n-k) \\$ funciones reales diferenciables $latex \rho_{1}, ..., \rho_{n-k}$ definidos en $latex U \\$, es decir:

$latex (\rho_{1}=0)\cap ... \cap (\rho_{n-k}=0)=M\cap U$

y $latex \forall p \in M \cap U$, los vectores

$latex \nabla \rho_{1}(p),...,\nabla \rho_{n-k}(p)$

son linealmente independientes y:

$latex T_{p}M= generado\lbrace \nabla \rho_{1}(p),...,\nabla \rho_{n-k}(p) \rbrace ^{\perp}$

y $latex dim(T_{p}M)=k$

Es fácil ver que la definición con curva suaves y la del espacio ortogonal de los gradientes son equivalentes, aquí esbozo la demostración:


Sea $latex \gamma:[-\epsilon,\epsilon]\rightarrow M$ con funciones coordenadas $latex \gamma_{1}, ... \gamma_{n}$

Y tenemos que $latex M \\$ está definida por las $latex f_{i} \\$ :

$latex f_{i}(\gamma_{1}(t), ..., \gamma_{n}(t)) = 0$     $latex \forall t \in [-\epsilon, \epsilon]$    $latex 1 \leq i \leq n-k$

Esto sucede porque la imagen de $latex Im(\gamma) \subset M$, si diferenciamos (jacobiana) con respecto a $latex t \\$  tenemos que por la regla de la cadena:

$latex \frac{\partial{f_{i}}}{x_{1}}(x(0))x_{1}\prime (0)+...+\frac{\partial{f_{i}}}{x_{n}}(x(0))x_{n}\prime (0)=0$    $latex \Leftrightarrow \nabla f_{i}(x(0)) \cdot x\prime (0)=0 \Leftrightarrow$ $latex \nabla f_{i}(x(0) \perp x\prime (0)$
$latex \square \\$

Ahora vamos definir el concepto final de este post para terminar de ver de que trata la estructura del espacio tangente.


Definicion: Denotemos por $latex (f,U)$ a un abierto de $latex M \\$ tal que $latex p\in U$ y $latex f \\$ diferenciable en $latex U$, decimos que:

$latex (f,U) \sim (g,V)$

Si en el abierto $latex U \cap V$ tenemos que $latex f=g$ , esto claramente es una relación de equivalencia por lo que podemos definir el espacio vectorial:

$latex C_{p}^{\infty} =\lbrace (f,U) \rbrace / \sim $

El espacio tangente $latex T_{p}M$ consiste en todos los mapeos lineales:

  $latex d:C_{p}^{\infty} \rightarrow C_{p}^{\infty}$

Tal que:

$latex d(fg)=fd(g)+gd(f)$

Es decir que cumplen la regla de Leibniz (son derivaciones!)

Este espacio es muy importante ya que captura las propiedades de funciones cercanas a $latex p \\$


Eduardo Ruiz Duarte (beck)
rduarte@ciencias.unam.mx
@toorandom

k-formas diferenciales y derivada exterior (Parte 2/2, k-formas diferenciales y derivada exterior de éstas)

Como vimos, las 1-formas elementales son la proyección en una coordenada, ahora veamos a los operadores diferenciales como k-formas en $latex \mathbb{R}^n$ donde sus coordenadas son $latex x_{1},x_{2},...,x_{n}$:

El punto de estos posts es poder hacer la construcción de las k-formas diferenciales en la topología de Zariski para poder justificar el cálculo de singularidades en variedades sobre cualquier campo algebraicamente cerrado de caracteristica p o 0
Y al final de este artículo construiremos con las k-formas diferenciales el rotacional, la divergencia y gradiente (hablando en términos de campos vectoriales en $latex \mathbb{R}^n$)

Sea $latex \mu=\lbrace i_{1}, ..., i_{k}\rbrace$ una subsucesión de
$latex \Omega = \lbrace 1,2,...,n \rbrace$, tal que $latex 1 \leq i_{1} < ... < i_{k} \leq n$  y sea


$latex \displaystyle dx_{\mu}=d{x_{i_{1}}}\wedge ... \wedge d{x_{i_{k}}}$

Una k-forma diferencial $latex \omega$ es:

$latex \omega = \sum_{|\mu|=k}{f_{\mu}dx_{\mu}}$

Donde $latex f_{\mu}$ es una función diferenciable, y $latex \mu \subset \Omega$ está ordenado de manera creciente y $latex |\mu|=k$, por ejemplo una 1-forma en $latex \mathbb{R}^{2}$:
$latex (x+cos(y))dx+xydy$


Y una 2-forma en $latex \mathbb{R}^{3}$

$latex e^{x+y}dx\wedge dz + y^{3}dy \wedge dz$


Cada k-forma diferencial define para todo punto en $latex \mathbb{R}^{n}$ una k-forma diferente por ejemplo la 1-forma $latex (x+sen(y))dx + xydy$ es la 1-forma $latex 3dx$ en el punto $latex (3,0)$ y es $latex 5dx+2\pi dy$ en el punto $latex (4,\frac{\pi}{2})$



Pa definir la derivada exterior, primero necesitamos ver que es la derivada exterior de una 0-forma (función diferenciable, es decir que esté definida bajo un operador diferencial... o sea un operador que cumpla la regla de Leibnitz, esto puede ser la derivada normal como la conocemos también) y por inducción se definirá la derivada exterior para una k-forma en general

Dada una función diferenciable (0-forma) $latex f(x_{1},...,x_{n})$, su derivada exterior será denotada como $latex d f$  y es:

$latex df=\sum_{i=1}^{n}{\frac{\partial{f}}{\partial x_{i}}dx_{i}}$


Por ejemplo:
Si $latex f(x,y)=xy-y^{3}$ su derivada exterior $latex d f$ es:

$latex df=ydx+(x+3y^{2})dx$



Esto se parece al gradiente (PARECE)
Ahora definiremos lo que es la derivada exterior de una k-forma $latex \omega = \sum_{|\mu|=k}{f_{\mu}dx_{\mu}}$ con  $latex \mu=\lbrace i_{1}, ..., i_{k}\rbrace$ ordenada creciente:


$latex d \omega = \sum_{|\mu|=k}{df_{\mu}\wedge dx_{\mu}} $

Veamos un ejemplo con la derivada de una 1-forma fácil:

Sea $latex \omega = f_{1}dx_{1} + f_{2}dx_{2} + f_{3}dx_{3}$ una 1-forma de $latex \mathbb{R}^3$, entonces:

$latex d \omega = df_{1}dx_{1}+df_{2}dx_{2}+df_{3}dx_{3}=$
$latex \Bigg ( \frac{\partial{f_{1}}}{\partial{x_{1}}}dx_{1}+\frac{\partial{f_{1}}}{\partial{x_{2}}}dx_{2}+\frac{\partial{f_{1}}}{\partial{x_{3}}}dx_{3} \Bigg )\wedge dx_{1}+$
$latex \Bigg ( \frac{\partial{f_{2}}}{\partial{x_{1}}}dx_{1}+\frac{\partial{f_{2}}}{\partial{x_{2}}}dx_{2}+\frac{\partial{f_{2}}}{\partial{x_{3}}}dx_{3} \Bigg )\wedge dx_{2}+$
$latex \Bigg ( \frac{\partial{f_{3}}}{\partial{x_{1}}}dx_{1}+\frac{\partial{f_{3}}}{\partial{x_{2}}}dx_{2}+\frac{\partial{f_{3}}}{\partial{x_{3}}}dx_{3} \Bigg )\wedge dx_{3}=$
$latex \Bigg ( \frac{\partial{f_{3}}}{\partial{x_{1}}} - \frac{\partial{f_{1}}}{\partial{x_{3}}} \Bigg ) dx_{1} \wedge dx_{3} + \Bigg ( \frac{\partial{f_{2}}}{\partial{x_{1}}} - \frac{\partial{f_{1}}}{\partial{x_{2}}} \Bigg ) dx_{1} \wedge dx_{2} + \Bigg ( \frac{\partial{f_{3}}}{\partial{x_{2}}} - \frac{\partial{f_{2}}}{\partial{x_{3}}} \Bigg ) dx_{2} \wedge dx_{3} $

Ufff.. imaginen escribir eso en latex inline en blogspot... pero bueno

Eso también se parece al rotacional del campo vectorial $latex (f_1,f_2,f_3)$ (PARECE)

Cómo ya se habrán dado cuenta para toda k-forma diferencial $latex \omega$ se tiene que $latex d(d\omega)=0$, eso lo pueden demostrar fácilmente suponiendo la anticonmutatividad del operador cuña y que el orden de diferenciación no afecta a la función diferenciable, es decir:

$latex \frac{\partial{}}{\partial{x_{i}}} \frac{\partial{f}}{\partial{x_{j}}} = \frac{\partial{}}{\partial{x_{j}}} \frac{\partial{f}}{\partial{x_{i}}}$ y que $latex dx_{i}\wedge dx_{j}=-dx_{j}\wedge dx_{i}$

Ahora como ven, hice hincapié en la palabra "parece" al decir que habíamos encontrado el rotacional y el gradiente en términos de k-formas, veamos cómo son estas cosas en $latex \mathbb{R}^3$ con coordenadas $latex x,y,z$, vamos a definir una funciones que nos ayudarán a que no "parezcan" sino que "sean"


Sean:
$latex \omega_{0}=f(x,y,z)$
una 0-forma

$latex \omega_{1}=f_{1}(x,y,z)dx+f_{2}(x,y,z)dy+f_{3}(x,y,z)dz$
una 1-forma en general

$latex \omega_{2}=f_{1}(x,y,z)dx\wedge dy + f_{2}(x,y,z)dx\wedge dz \wedge f_{3}(x,y,z)dy\wedge dz$
una 2-forma elemental general

Y como la única 3-forma elemental en $latex \mathbb{R}^{3}$ es $latex dx\wedge dy\wedge dz$ tenemos que una 3-forma elemental general sería de la forma:

$latex \omega_{3}=f(x,y,z)dx\wedge dy \wedge dz$

Donde $latex f_{i},f\in \mathfrak{F}(\mathbb{R}^{3})$ (funciones en $latex \mathbb{R}^{3}$)

Definimos las siguiente funciones: entre formas y funciones de $latex \mathbb{R}^{3}$ denotadas por $latex \mathfrak{F}(\mathbb{R}^{3})$ y formas con campos vectoriales de $latex \mathbb{R}^{3}$ denotadas por $latex \Delta(\mathbb{R}^{3})$

$latex \displaystyle \theta_{0}: {\bigwedge}^{0}{\mathbb{R}^{3}} \rightarrow \mathfrak{F}(\mathbb{R}^{3})$

    $latex \omega_{0} \mapsto f$

$latex \displaystyle \theta_{1}: {\bigwedge}^{1}{\mathbb{R}^{3}} \rightarrow \Delta(\mathbb{R}^{3})$

    $latex \omega_{1} \mapsto (f_{1},f_{2},f_{3})$

$latex \displaystyle \theta_{2}: {\bigwedge}^{2}{\mathbb{R}^{3}} \rightarrow \Delta(\mathbb{R}^{3})$

    $latex \omega_{2} \mapsto (f_{3},-f_{2},_f_{1})$

$latex \displaystyle \theta_{3}: {\bigwedge}^{3}{\mathbb{R}^{3}} \rightarrow \mathfrak{F}(\mathbb{R}^{3})$

    $latex \omega_{3} \mapsto f(x,y,z)$

Esto ¿para qué?, como vemos $latex \theta_{0}$ es la identidad y estas definiciones tienen una manera natural de ser, ya que si hacen la talachita pueden demostrar el siguiente teorema:

Teorema: En $latex \mathbb{R}^{3}$, si $latex \omega_{s}$ es una s-forma entonces

$latex \theta_{1}(d\omega_{0})=\nabla \theta_{0}(\omega_{0})=\vec{\nabla f}=grad(\theta_{0}(\omega_{0}))$
$latex \theta_{2}(d\omega_{1})=\nabla \times \theta_{1}(\omega_{1})=rot({\theta_{1}(\omega_{1})})$
$latex \theta_{3}(d\omega_{2})=\nabla \cdot \theta_{2}(\omega_{2})=div({\theta_{2}(\omega_{2})})$
$latex \square$

Cada uno de los cálculos se puede hacer explícitamente y no hay mucho que pensar en la demostración más que talacha dura, y con esto tenemos ya en términos de formas diferenciales lo que es el gradiente, rotacional y divergencia

El punto de estos posts es poder llegar a definir esto en términos de geometría algebraica en variedades usando la topología de Zariski

Eduardo Ruiz Duarte (beck)
rduarte@ciencias.unam.mx
@toorandom

k-formas diferenciales y derivada exterior (Parte 1/2, k-formas $latex \wedge$)

Estos conceptos son de suma importancia en varias areas de matemáticas, no sólo en geometría diferencial, también en geometría algebraica por ejemplo al definir espacios tangentes con la topología de Zariski, pero también he visto que hay ciertas confusiones, por lo que trataré de dejar el concepto claro con lo que sé y mis notas del curso de geometría diferencial que tomé con el Dr. Gregor Weingart.
Para esto primero veremos lo que son las k-formas y el producto cuña en esta primera parte. 

Estoy suponiendo que el lector tiene conocimiento de lo que significa el determinante en términos de volumen, a grandes rasgos si tú tienes vectores en un espacio de Banach donde sí se vale el teorema de Ptolomeo (La relación entre los lados de un paralelogramo y sus diagonales), estos espacios de Banach son espacios de Hilbert y pueden dar luz a un único producto interno, y con este al determinante, ejemplos de estos espacios son los famosos $latex \mathbb{R}^n$ y $latex \mathbb{C}^m$, así que regresando al determinante formando la matriz $latex A=(v_1,...,v_k)$
y consideras $latex A^{T}$ entonces el volumen del paralelepípedo generado por los vectores $latex \lbrace v_1, ..., v_k \rbrace$ es $latex \sqrt{det(A^{T}A)}$, si te cuesta trabajo visualizarlo, imagina sólamente un vector $latex A=v \in \mathbb{R}^{n}$ , tenemos que $latex \sqrt{det(A^{T}A)}=\sqrt{det(v\cdot v)}=\sqrt{det({a_1}^{2}+...+{a_n}^{2})}=\sqrt{{a_1}^{2}+...+{a_n}^{2}}=||{v}||$
el cual pues es el "volumen" (longitud) del vector.

Trataremos primero de entender 2-formas elementales en $latex \mathbb{R}^3$, y llamaremos $latex x_1,x_2,x_3$ los ejes coordenados de $latex \mathbb{R}^3$. Ahí tendremos tres 2-formas elementales que serán denotadas por $latex dx_1 \wedge dx_{2} , dx_{1} \wedge dx_{3}, dx_{2} \wedge dx_{3}$

En palabras burdas, $latex dx_{i} \wedge dx_{j}$ es un operador que es el area (con signo) de la proyección en el plano $latex x_{i}x_{j}$ de un paralelepípedo en  $latex \mathbb{R}^3$.

Como ejemplo, a mi me lo explicaron siempre suponiendo que ya lo conocía... a veces necesito ejemplos para poder entender lo que me están diciendo o demostrando.

Considera los vectores $latex {v_{1}}^{T}=(1,2,3)$ y $latex {v_{2}}^{T}=(3,2,1)$ , si los dibujan verán que forman un paralelepitedo $latex P$ en $latex \mathbb{R}^3$, considera la proyección:

$latex \rho : \mathbb{R}^3 \rightarrow \mathbb{R}^2$
$latex (x_1,x_2,x_3) \mapsto (x_1,x_2)$

Es decir de $latex \mathbb{R}^3$ al plano $latex x_{1} x_{2}$

Definimos $latex dx_{1} \wedge dx_{2}$ actuando en el paralelepípedo $latex P$ como el area de
$latex \rho(P)$ es decir:

$latex dx_{1}\wedge dx_{2}(P)=A(\rho (P) )$

Entonces tenemos que $latex \rho(P)$ es el paralelogramo en este ejemplo formado por $latex \rho(v_{1})$ y $latex \rho(v_{2})$ es decir por los vectores $latex (1,2)$ y $latex (3,2)$

Esto nos dice que:

$latex dx_{1} \wedge dx_{2}(P)=det(\rho(v_{1}),\rho(v_{2}))= det\begin{pmatrix} 1& 3\\2&2 \end{pmatrix}=-4$

En general en $latex \mathbb{R}^{3}$ , dados dos vectores columna que forman un paralelogramo $latex v_{1}^{T}$ y $latex v_{2}^{T}$ para la matriz $latex A=(v_{1}^T,v_{2}^T)=\begin{pmatrix} a_{11}&a_{12}\\a_{21}&a_{22}\\a_{31}&a_{32} \end{pmatrix}$
Tenemos que el area del paralelogramo en la proyección en el plano $latex x_{1}x_{2}$ es:

$latex dx_{1}\wedge dx_{2}(A)=det \begin{pmatrix} a_{11}& a_{12}\\a_{21}&a_{22} \end{pmatrix}$

De manera similar para los planos $latex x_{i}x_{j}$

Ahora, cuando vemos una integral $latex \int{f(x)}dx$ el significado de dx lo puedes deducir como una 1-forma que es la longitud en el eje x, este operador es el "volumen" en una dimensión como lo mencioné al inicio de este post, el "volumen" aquí es la longitud, por lo que:

Si $latex v=(a_{i},a_{j},a_{k})$ entonces $latex dx_{s}(v^{T})=a_{s}$ el cual es la proyección $latex \rho_{s}$ en la s-ésima coordenada.

Ahora cómo generalizamos esto a k-formas?, es decir, este operador $latex \wedge$ queremos que nos calcule el volumen de paralelepípedos k-dimensionales en un espacio de Hilbert n-dimensional, en este caso usamos $latex \mathbb{R}^{n}$

Para la generalización en $latex \mathbb{R}^{n}$ , tenemos que si sus coordenadas son $latex x_1,x_2,...,x_n$ Si tenemos una subsucesión $latex \Omega=(i_1,i_2,..,i_k)$ de tamaño $latex k$ de $latex (1,2,...,n)$ donde $latex 1\leq i_{1}< ...< i_{k} \leq 1$
$latex A=\begin{pmatrix} a_{11}&a_{12}&\cdots &a_{1k}\\ \vdots&\vdots&\vdots &\vdots\\ a_{n1}&\cdots &\cdots& a_{nk} \end{pmatrix}=\begin{pmatrix}A_{1}\\ \vdots \\ A_{k}\end{pmatrix}$ Es una matriz de $latex n\times k$ donde sus columnas generan el paralelepípedo k-dimensional en $latex \mathbb{R}^{n}$, denotamos sus renglones por $latex A_{i}$
Lo que queremos es un operador que actúe en la matriz $latex A$ para darnos el (hiper)volumen del paralelepipedo proyectado en el (hiper)espacio $latex {x_{i}}_{1} {x_{i}}_{2}...{x_{i}}_{k}$ por lo que la k-forma es el siguiente operador:

$latex \displaystyle dx_{\Omega}=d{x_{i}}_{1} \wedge d{x_{i}}_{2}\wedge ...\wedge d{x_{i}}_{k}$

Donde

$latex \displaystyle {dx}_{\Omega}(A)=d{x_{i}}_{1} \wedge d{x_{i}}_{2}\wedge ...\wedge d{x_{i}}_{k}(A)=det \begin{pmatrix}A_{i_{1}}\\ \vdots \\ A_{i_{k}}\end{pmatrix} $

Ya con esto es suficiente para que puedas comenzar a jugar, es decir... este producto es conmutativo ?
La respuesta es NO, depende, pero no es tan grave, es anticonmutativo en el caso de 1-formas esto es porque para un paralelepípedo P
$latex dx_{i} \wedge dx_{j}(P)=det(\rho(v_{i}),\rho(v_{j}))=-det(\rho(v_{j}),\rho(v_{i}))=-dx_{j} \wedge dx_{i}(P)$
al final es una propiedad elemental de matrices, al cambiar columnas o renglones se alterna el signo, por lo que tenemos que este es un operador alternante
, ahora, aquí usamos el determinante, pero todos los operadores que tengan las características del determinante serán k-formas

De hecho decimos que una k-forma real $latex \omega$ sobre $latex \mathbb{R}$ es es una función:

$latex \omega :M_{nk}(\mathbb{R})\rightarrow \mathbb{R}$

Que satisface multilinearidad, lo cual se expresa usando como argumento para $latex \omega$ la matriz de $latex n\times k$ separada por columnas $latex \Lambda=(A_{i},...,\lambda B + \mu C,...,A_{k})$:

$latex \omega(\Lambda)=\omega(A_{1},...,\lambda B+ \mu C, ..., A_{k})=\lambda \omega(A_{1},...,B,...,A_{k})+\mu \omega(A_{1},...,C,...,A_{k})$

Es decir las propiedades del determinante, pero estas funciones alternantes son en general, es por eso que a las k-formas primeras les llamamos "elementales" , pero estas son las generales.

Ya con esto el teorema principal que no demostraré, pero ya se imaginarán el por qué de su veracidad es el siguiente:

Teorema: Las k-formas del espacio vectorial $latex \mathbb{R}^{n}$ forman un espacio vectorial de dimensión $latex \begin{pmatrix}n\\ k\end{pmatrix}$ donde las k-formas elementales forman una base para éste, este espacio vectorial se denota como $latex \displaystyle {\bigwedge}^{k}(\mathbb{R}^{n})$
$latex \square$

Ahora, si $latex \tau,\sigma$ son l-forma y k-forma respectivamente tenemos que
$latex \tau \wedge \sigma = (-1)^{lk}\sigma \wedge \tau=0 \Leftrightarrow l,k$ son impares

(en el caso de 1-formas por eso se alterna el signo) esto es fácil demostrarlo con lo que hemos visto, sólo tienes que desarrollar el producto cuña bien con una k-forma y una l-forma en general

Ahí se ve lo que pasa con la alternancia. Para esto puedes demostrar que el producto cuña ($latex \wedge$) de dos 1-formas te da 2-formas, y con las propiedades de alternancia y multilinearidad podemos definir lo que es una k-forma diferenciable y la derivada exterior, pero esto lo veremos en la parte 2 de este post
Espero les haya servido de algo
Eduardo Ruiz Duarte(beck)
rduarte@ciencias.unam.mx