Si estás desde un smartphone haz click aquí para que se vea mejor.
http://b3ck.blogspot.mx/2014/07/grupos-de-trenzas.html?m=0
Vamos a introducir una noción de Artin que generaliza de cierta forma el grupo simétrico $latex S_n$ de permutaciones, los grupos de trenzas son interesantes porque también tienen una noción geométrica intuitiva que nos va a llevar a su presentación algebraica, el grupo de trenzas de orden $latex n$ será denotado por $latex B_n$ (la $latex B$ es por braid), pero vamos a empezar al revés... daremos una noción intuitiva, un ejemplo y al final daremos la definición formal y veremos que hay usos que se le pueden dar en criptografía.
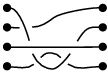
Lo que vamos a estudiar son configuraciones de "hebras" (hilos) que se ven de esta forma, y ver cómo hacerlas interactuar unas con otras para generar una estructura algebraica que como dijimos anteriormente, generaliza al grupo de permutaciones $latex S_n$ también definido por Emil Artin
Imaginemos que tenemos $latex n=4$ hilos, donde los extremos de cada uno de los 4 hilos están fijos con unos clavos, todas las configuraciones que podamos hacer con 4 hilos que no hagan nudos serán elementos de $latex B_4$ veamos a qué me refiero con esto.
Por ejemplo:
Noten la diferencia de las hebras en cuanto a cuál pasa por encima de la otra.
También podemos ver que dibujándolas, las podemos hacer tan complejas como sean, pero al final siempre habrá una manera de dibujarlas de manera simple, es donde entra la abstracción del concepto ya que por ejemplo:
Y no se valen cosas como estos nudos:
Pero ¿por qué le llamamos grupo? , es decir, sabemos que un grupo es una estructura algebraica la cual contiene objetos que pueden interactuar con una operación binaria dando como resultado otros objetos de la misma estructura (cerradura), existe un objeto que es neutro, es decir que deja invariante a todos los elementos bajo la operación binaria y cada uno de los elementos tiene un inverso con esa operación que al usar la operación binaria entre inversos te da como resultado el neutro y es asociativo (como los números enteros bajo la suma)
$latex B_n$ no será abeliano para $latex n>2$ es decir sus elementos no conmutarán, veamos cómo funciona esta operación de $latex B_4$
La manera en la que vamos a sumar dos trenzas $latex \sigma \oplus \tau = \omega \in B_4$ veámosla con un par de ejemplos
$latex \sigma$ $latex \tau$ $latex \omega$
Observen como se hace la suma, que es "siguiendo" la trayectoria de las hebras en $latex \sigma$ , fijense como se cruzan unas con otras, pero bueno este ejemplo es muy intuitivo, algo un poco más interesante que servirá para que demuestren qué sucede con $latex B_2$ es el siguiente.
$latex \sigma_1$ $latex \sigma_2$ $latex \sigma_3$
Como pueden ver este ejemplo es menos trivial, pueden ver que las dos hebras de arriba se desenrredan
pero las dos de abajo una pasa por encima de otra, y al seguir la trayectoria con $latex \sigma_2$ vemos que pasa por abajo y se hace una trenza en $latex \sigma_3$
Con este ejemplo es fácil ver que $latex B_n$ es infinito con $latex n>1$ ya que las trenzas se pueden enredar cuantas veces quieras, y también se puede ver que $latex B_4$ no es abeliano ya que puedes experimentar un poco con estos ejemplos y verás que te dan elementos diferentes a $latex \omega$ o a $latex \sigma_3$
Pero bueno... ya basta , vamos a representar la infinidad de elementos de $latex B_4$ , para eso es el álgebra no? , no nos da miedo que sean infinitos.
Para poder construir explícitamente la estructura de $latex B_4$ primero tenemos que observar cuáles son las trenzas básicas que nos servirán para representar TODOS los elementos de $latex B_4$ , es decir , de quién son combinaciones.
Consideremos
 |  |  |
Todas las trenzas en $latex B_4$ pueden escribirse como composición de estas trenzas y sus inversos, o sea que si $latex \sigma\in B_4$ entonces su inverso $latex \sigma^{-1}$ será el elemento tal que $latex \sigma\oplus \sigma^{-1}=0$ donde 0 es la trenza que no tiene cruces, es decir todas las hebras son paralelas.
Para ver que cada trenza $latex \tau \in B_4$ es combinación de $latex \sigma_1,\sigma_2,\sigma_3$ y sus inversos, toma una trenza $latex \tau$ arbitraria y comienza a examinar de izquierda a derecha los cruces comenzando de la hebra de hasta arriba, cada que encuentres un cruce de las hebras $latex i$ y $latex i+1$ escribe $latex \sigma_i$ si la hebra $latex i$ pasa por arriba de $latex i+1$ o $latex \sigma_i^{-1}$ si pasa por abajo, y así vas escribiendo todo como la suma de éstos con $latex \oplus$
cuando termines de examinar cada hebra hasta el clavo final de la parte derecha, habrás construido la combinación de estas $latex \sigma_i$'s , y es intuitivo ya que estos generadores son los cruces fundamentales.
Si observas puedes ver que:
-
- (i) $latex \sigma_1\oplus\sigma_3=\sigma_3\oplus\sigma_1$
-
- (ii) $latex \sigma_1\oplus \sigma_2\oplus \sigma_1= \sigma_2\oplus \sigma_1\oplus \sigma_2$
- (ii) $latex \sigma_2\oplus \sigma_3\oplus \sigma_2= \sigma_3\oplus \sigma_2\oplus \sigma_3$
Y si no te percataste es fácil que lo veas con una hoja de papel.
Por lo que ya tenemos cómo es $latex B_4$ pero estas identidades se pueden extender en general para $latex B_n$
por lo que:
$latex B_n :=$ < $latex \sigma_1, \sigma_2,...,\sigma_n \mid \sigma_i \oplus \sigma_{i+1}\oplus \sigma_i = \sigma_{i+1}\oplus \sigma_i \oplus \sigma_{i+1}$ con $latex 1\leq i \leq n-2$ , $latex \sigma_i\oplus \sigma_j = \sigma_j \oplus \sigma_i$ con $latex \mid i-j \mid \geq 2$ >
Este grupo ha sido estudiado para criptografía , por David Garber http://arxiv.org/pdf/0711.3941.pdf
Pero desafortunadamente fue roto hace unos años, pero la teoría no deja de ser interesante, ya que se le puede asociar el grupo fundamental (Topología algebraica) de ciertos espacios, y encontrar de quién es el grupo fundamental es lo interesante.
También es interesante investigar cómo $latex B_3$ está relacionado al grupo especial lineal $latex SL(2,\mathbb{Z})$
Y como pendiente queda el grupo de trenzas con 2 hebras $latex B_2$ , pero pues... éste está generado por 2 elementos que son uno inverso de otro, es decir por 1 elemento... que es la trenza simple con dos hebras.... por lo que sólo se pueden generar trenzas con 2,3,4,... vueltas, pero también las puedes deshacer con su inversa , es decir
$latex B_2 \cong$ < $latex \mathbb{Z},+$> = < $latex1,-1$ >
Este es el único grupo de trenzas no trivial que es abeliano y como pueden ver no tiene mucho chiste.
Espero que les haya gustado, las imágenes las saqué de wikipedia y del artículo de David Garber antes mencionado.
Eduardo Ruíz Duarte
Twitter: @toorandom











1 comment:
Thank you ffor writing this
Post a Comment