El post siguiente que es la parte 1.5/2 es la construcción de los grupos de cohomología usando los grupos de homología que definiremos enseguida.
Poincaré fue el primero que comenzó con la teoría de homología y cohomología, pero no como lo conocemos ahora, él trabajaba con topología y lo que él quería era contar hoyos , esto podrá sonar muy trivial si se imaginan un toro o una esfera que saben que tiene 1 hoyo y 0 hoyos respectivamente, pero como se imaginarán existen espacios muy complicados, que en la práctica por ejemplo se puede traducir a superficies modeladas con ecuaciones que representan restricciones en un modelo de muchas dimensiones... si quieres imaginarte su geometría, estarás perdido, para eso tienes que fijarte en su topología para poder tener una intuición de cómo se ve, o sea yo te puedo decir que la ecuación $latex y^2 = x^3 - 1$ así de simple como la ves tiene un hoyo en $latex \mathbb{C}^2$ a pesar de que estos hoyos no se puedan visualizar tan intuitivamente.
La técnica de medir estos hoyos, que al final serán invariantes topológicos se basa en muchas cosas, entre ellas la teoría de homología y cohomología las cuáles de manera tonta la puedes ver como cierta álgebra extraída de la topología del objeto.
Ya hemos hablado antes de cohomología de deRham aquí o de cohomología de grupos acá para extender este concepto de hoyos a objetos algebraicos a través de la cohomología de Cech, también tratamos de dar la idea de Cohomología usando cálculo aquí por lo que voy a suponer que algunos conceptos ya son claros aunque tal vez repita algunos aquí.
El concepto de dualidad de Poincaré es un resultado topológico que relaciona los grupos de homología y cohomología de una variedad $latex V$ cerrada orientable de dimensión $latex n$ (sin frontera como una circunferencia, toro o esfera $latex \mathbb{S}^2$ ) , de hecho dice que
$latex H_{n-k}(V) \cong H^{k}(V)$
Es decir que el $latex k-$ésimo grupo de cohomología es isomorfo al $latex n-k$-ésimo grupo de homología de una variedad orientable y cerrada $latex V$.
Poincaré no definió el teorema anterior así, de hecho él lo definió en términos de números de Betti, (Enrico Betti) , estos números los bautizó Poincaré en su honor ya que Betti estudió superficies sin frontera en dimensiones altas lo cual fue el motivante para Poincaré, y los definió así:
Definición
Sea $latex V$ una variedad de dimensión $latex n$ el número de Betti $latex B_r$ para una dimensión $latex r$ es el número máximo de subvariedades de $latex V$ de dimensión $latex r$ contenidas en $latex V$ que son linealmente independientes, +1
Teorema de dualidad de Poincaré: Si $latex V$ es de dimensión $latex n$ orientable y cerrada entonces $latex B_r=B_{n-r}$
Este tipo de resultados tienen aplicaciones en física cuántica y en estudio de la forma del universo, entre otras cosas que no conozco bien pero que bien si les interesa pueden investigarlo ustedes mismos y verán por qué en un momento.
También existe otra relación geométrica que es muy familiar para nosotros, que es la característica de Euler, tal vez algunos han experimentado con la fórmula característica de Euler
$latex \chi=V-E+F$ , es decir vértices-aristas+caras , este número es interesante, ya que es un invariante topológico, si ustedes triangulan, cuadriculan, o dibujan cualquier red de aristas, vértices y caras en una esfera, SIEMPRE obtendrán $latex \chi=2$ , es decir una esfera triangulada y cuadriculada les dará 2, o si aplican la fórmula a un octaedro y a un cubo también... pero si aplican la fórmula a un toro triangulado o a una botella de Klein, verán que las cosas cambian, ya que no son topológicamente equivalentes a una esfera y obtendrán otros valores porque tienen hoyos.
De hecho, esto puede ser generalizado a dimensiones altas, y lo que dice aquí se puede pasar a complejos de cadena, una cara es la frontera de una variedad, la frontera de una cara son las aristas, y la frontera de una arista son sus vértices $latex (V\leftarrow E \leftarrow F)$ y cuál es la frontera de una frontera ?, es decir si $latex X$ es una variedad y $latex \partial$ es el operador que te calcula la frontera qué es $latex \partial\partial X$ ? , si saben un poco de topología puntual, saben que la frontera de un objeto es un conjunto cerrado sin puntos interiores... por lo tanto la frontera de esto al no haber puntos interiores deberá ser vacía (no hay de donde tomar orilla).
La generalización de esto, es decir ya no podemos hablar de aristas, caras ni vértices, sino de símplices, porque en dimensiónes más altas que 3 necesitarías otras palabras como "hipercara".
Teorema: Sea $latex U$ una variedad de dimensión $latex n$
$latex \chi_U = \sum_{r=0}^n (-1)^{r}\Delta_r = \sum_{r=0}^n (-1)^{r}B_r$
La parte izquierda es la misma formula característica de Euler, $latex V-E+F$ pero en general para una variedad $latex U$ de cualquier dimensión $latex n$, donde $latex \Delta_r$ son los símplices de dimensión $latex r$ tomados en cualquier triangulación definida en $latex U$ (si $latex n=3$ entonces tienes la formula usual de Euler) , en la parte derecha tenemos los números de Betti de $latex X$ para cada una de las dimensiones $latex r$.
De hecho a Platón o algún otro filósofo-matemático griego se les escapó una oportunidad de pasar aún más a la historia al estudiar los sólidos tridimensionales, sería considerado padre de la homología, ya que si hubiera dicho algo así como "La frontera de la frontera es vacía" seguro hubiera pasado a la historia de las matemáticas como lo hizo Euclides y muchos teoremas importantes en topología algebraica llevarían su nombre, de hecho en todas las teorías de Homología y Cohomología se necesita tener un operador frontera $latex \partial$
Este resultado de Poincaré trataré de explicarlo sólo como una motivación que pretenderá dar una intuición geométrica-topológica de esto, pero para esto tendré que explicar un poquito de homología simplicial que es la más básica, pero es la necesaria para poder entender construcciones más ricas como la homología singular.
Definición
Un $latex k-$símplice $latex \Delta_k$ es un triángulo generalizado a dimensión $latex k$, y es la envolvente conexa de $latex k+1$ puntos en $latex \mathbb{R}^{k+1}$ , es decir, es la intersección de todos los conjuntos convexos que contienen a esos puntos.
Más fácil, es un triángulo generalizado, si $latex k=2$ tenemos que en $latex \mathbb{R}^{3}$ necesitamos $latex 2+1$ puntos para definir un $latex 2-$símplice , es decir.. un triángulo, un triángulo es el conjunto $latex \Delta_2=\lbrace (x_0,x_1,x_2)\in \mathbb{R}^3 : x_0+x_1+x_2=1,\space x_0,x_1\geq 0\rbrace$, en general
$latex \Delta_n=\lbrace (x_0,...,x_n)\in \mathbb{R}^{n+1} : \sum_{i=0}^{n}x_i=1, \space x_i\geq 0\rbrace$
Ése señoras y señores es un triángulo de dimensión $latex n$ generalizado, noten que lo expresamos en dimensión $latex \mathbb{R}^{n+1}$, podrían usar otro espacio euclídeo, no sólo $latex \mathbb{R}^k$, para $latex \Delta_0$ tenemos que $latex x_0=1$ es un punto, después $latex \Delta_1$ es una recta, $latex \Delta_2$ es un triángulo, $latex \Delta_3$ es un tetraedro, $latex \Delta_4$ es un pentatopo, etc... y este objeto es la base de la triangulación de cualquier variedad., noten que los puntos $latex v_0=(1,0,0...0) ,v_1=(0,1,0,0,...0), v_n=(0,0,...,0,1)$ son parte del conjunto y les llamamos coordenadas baricéntricas y son los vértices del $latex n-$símplice y nos permiten de una manera referirnos a los símplices sólo identificados con estos puntos.
Definición (complejo simplicial): Un $latex \Delta-complejo$ simplicial es un conjunto de símplices de cualquier dimensión, pegados de tal manera que sus intersecciones también son símplices,
Vamos a denotar como $latex \Delta^{\alpha}_k$ como al $latex k-$símplice indexado por $latex \alpha$ , es decir denotar a la arista1, arista2, cara8, etc...
Es decir, un complejo simplicial es un conjunto de simplejos (puntos, aristas, triangulos, tetraedros, et cétera) , que cumplen que si $latex \sigma \in \mathcal{K}$ entonces las caras de $latex \delta$ también están en $latex \mathcal{K}$ y que si $latex \sigma_1,\sigma_2\$ pertenecen al complejo simplicial entonces $latex \sigma_1\cap \sigma_2$ también es una símplice común (cara común, arista común, vértice común, tetraedro común).
Ejemplo complejo simplicial No-Ejemplo complejo simplicial
Ya con esto definimos los objetos en los cuales nos vamos a enfocar, ahora vamos por el álgebra aquí.
Definición (k cadena): Sea $latex X$ un $latex \Delta-$complejo simplicial, una $latex k-$cadena es una combinación lineal de $latex k-$símplices vista desde el grupo abeliano libre $latex \Delta_k(X)$ tomando como base todos los $latex k-$símplices de $latex X$, es decir es una $latex k-$cadena es una expresión de la forma
$latex \sum_{i=0}^{n} n_i\Delta^{i}_k$
Es decir por ejemplo es una expresión como $latex 4\Delta^{1}_3+8\Delta^{2}_3$ sería una $latex 3-$cadena formada por dos tetraedros.
Definición (k frontera débil): La $latex k$-frontera de una $latex k$-cadena es la suma de los $latex k-1$-simplices en la $latex k$-cadena, la cual se obtiene al quitar una coordenada a cada uno de los $latex k-$símplices de la $latex k$-cadena.
Vamos a desarrollar más esto que es importante, es décir como calcular la frontera.
Si tenemos un $latex k$-símplice, sabemos que está dado por sus coordenadas baricéntricas, que son los vértices, entonces
$latex \Delta_k = [v_0,v_1,...,v_k]$
Si queremos calcular su frontera de esta $latex k$-cadena, como dijimos en la definición, es calcular la $latex k-1$-cadena quitando vértices de $latex \Delta_k$ es decir.
$latex Fr(\Delta_k) = \sum_{i} [v_0, ..., \hat{v_i}, .. v_k]$
Donde $latex \hat{v_i}$ significa quitar esa coordenada, y vamos a modificar la función de frontera anterior y substituirla por una $latex \partial$ que nos permitirá conservar orientación de las caras, aristas, etc..
$latex \partial\Delta_k = \sum_{i} (-1)^{i}[v_0, ..., \hat{v_i}, .. v_k]$
Por ejemplo, podemos ver como se calcula la frontera de una arista, cara y tetraedro en la siguiente imagen sacada del libro de topología algebraica de Hatcher
Aquí pueden ver cómo se ve la frontera de una arista $latex [v_0,v_1]$ et cétera
Definición (k-frontera fuerte)
La función de frontera definida entre los $latex k$-simplices y $latex k-1$-simplices de una complejo simplicial $latex X$, donde definimos $latex \Delta_k(X)$ como el grupo abeliano libre formado por los $latex k-$simplejos está definida como:
$latex \partial_k:\Delta_k(X)\rightarrow \Delta_{k-1}(X)$
$latex \Delta^{\alpha}_k \mapsto \sum_{i}(-1)^{i} \Delta^{\alpha}_k\mid [v_0,...,\hat{v_i},...,v_k]$
Donde es fácil ver que el lado derecho en efecto es una $latex k-1$-cadena porque sólo estamos sumando las mismas coordenadas de $latex \Delta^{\alpha}_k$ pero quitándole una coordenada, convirtiéndola en una $latex k-1$-cadena.
Es un ejercicio usual que prueben el siguiente teorema
Teorema: La composición en:
$latex \Delta_n(X)\xrightarrow{\partial_n}\Delta_{n-1}(X)\xrightarrow{\partial_{n-1}}\Delta_{n-1}(X)$
Es 0, es decir $latex (\partial_{n-1}\circ \partial_{n})(\Delta_{n}^{\alpha})=0$ para cualquier $latex \Delta_{n}$ y $latex \forall n$
De hecho esto es la algebrización de lo que Euclides o Platón pudieron haber hecho para pasar a la historia de La frontera de la frontera es vacía, esto sucede en cualquier dimensión y para cualquier símplice en cualquier complejo simplicial.
Definición (k ciclo): Un $latex k$-ciclo es una $latex k$-cadena cuya $latex k$-frontera es 0, y de hecho los $latex k-$ciclos son un subconjunto de las $latex k$-cadenas.
Tenemos que $latex Im\partial_n \subset Ker \partial_{n-1}$ y de hecho los $latex n-$ciclos coinciden con $latex Im\partial_n$ y las $latex n$-fronteras coinciden con $latex Ker \partial_{n-1}$
como todo lo estamos trabajando en el grupo abeliano libre $latex \Delta_k{X}$ para cualquier $latex k$ , podemos definir el cociente, y tenemos la siguiente definición.
Definición (n-ésimo grupo de Homología)
El $latex n$-ésimo grupo de Homología de $latex X$ es:
$latex H_n(X)=ker\partial_{n}/im\partial_{n+1}$
Ejemplo $latex \mathbb{S}^2$
El ejemplo obligado es $latex X=\mathbb{S}^1$ el círculo, donde tomas sólo un vértice $latex v$ y una arista $latex e$ que se cierra a si misma para que sea más simple, entonces puedes ver que de hecho $latex \Delta_0(X)$ el grupo abeliano libre generado por un vértice , y $latex \Delta_1(X)$ el generado por una arista pues es simplemente $latex \mathbb{Z}$ , para dimensiones más altas es 0, porque no hay símplices más grandes que quepan en el círculo.
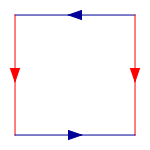
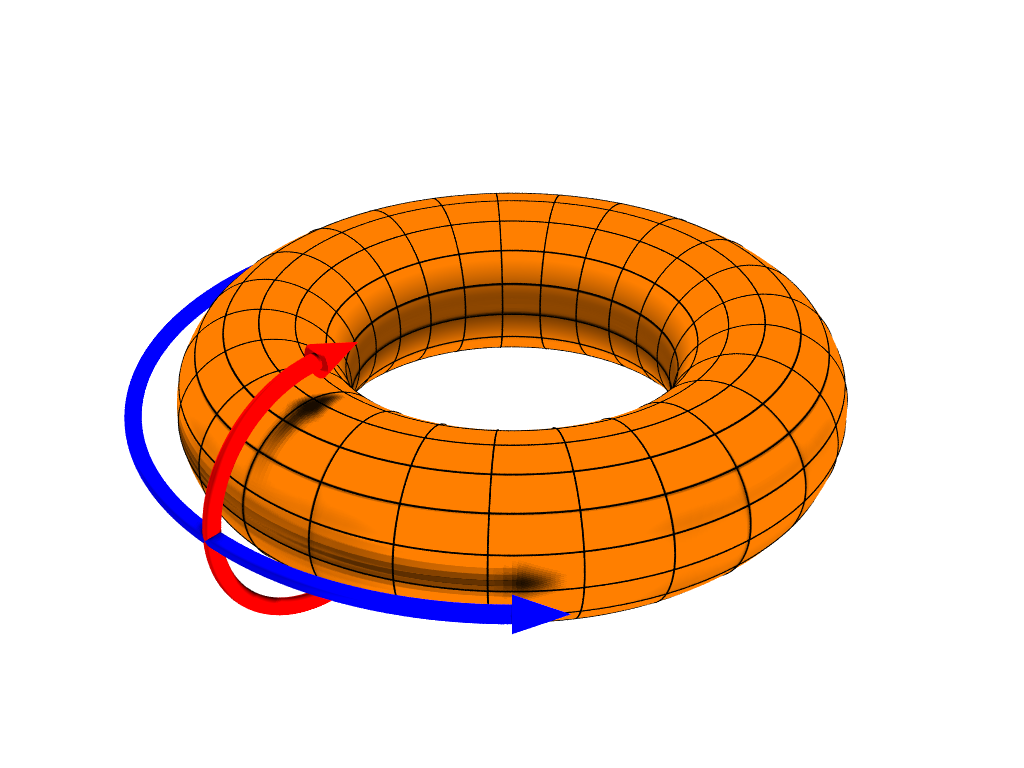
Ejemplo toro (dona):
Otro ejemplo que pueden desarrollar es el Toro, donde deberían de obtener $latex H_1(T)=\mathbb{Z}\oplus\mathbb{Z}$ , y como hint pueden usar la definición básica del toro con flechas
Que significa , "doblar y pegar las aristas azules y despues doblar y pegar las aristas rojas", como pueden ver en el siguiente dibujito, eso ya les define una configuración básica de tres aristas (1-símplices) $latex a,b,c$ también dos caras $latex U,L$ (2-símplices) y un solo vértice $latex v$ (0-símplice), lo cual es suficiente para calcular homología, recuerden que todo esto es invariante bajo configuraciones de triangulaciones, y realmente estarían calculando la homología de lo azul con lo rojo con la siguiente configuración donde solo hay un solo vértice.
De hecho $latex \partial_1=0$ como en el ejemplo pasado haciendo que $latex H_0(T)=\mathbb{Z}$ y $latex \partial_2(U)=\partial_2(L)=a+b-c$ y $latex \lbrace a,b,a+b-c\rbrace$ es base $latex \Delta_1(T)$ por lo que $latex H_1(T)=\mathbb{Z}\oplus \mathbb{Z}$, todo esto lo pueden verificar ustedes, pero esto lo debi de haber dejado como ejercicio.
Espero les haya gustado, la siguiente parte veremos ya el teorema de dualidad de Poincaré
Eduardo Ruíz Duarte (beck)
twitter: @toorandom


No comments:
Post a Comment